Advertisements
Advertisements
Question
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to the fixed, and neglect air resistance.
Solution 1
No
Range, R = 3 km
Angle of projection, θ = 30°
Acceleration due to gravity, g = 9.8 m/s2
Horizontal range for the projection velocity u0, is given by the relation:
R = `(u^2_0sin2theta)/g`
`3 = u_0^2/g sin 60^@`
`u_0^2/g =2sqrt3` ..(i)
The maximum range (Rmax) is achieved by the bullet when it is fired at an angle of 45° with the horizontal, that is,
`R_"max" = (u_0^2)/g` ..(ii)
On comparing equations (i) and (ii), we get:
`R_"max" = 3sqrt3 = 2 xx 1.732 = 3.46 km`
Hence, the bullet will not hit a target 5 km away
Solution 2
Here R = 3 km = 3000 m, `theta = 30^@`, g = 9.8 `ms^(-2)`
As R = `(u^2sin 2theta)/g`
`=> 3000 = (u^2sin 2 xx 30^@)/9.8 = (u^2sin 60)/9.8`
`=> u^2 = (3000xx 9.8)/(sqrt3"/2") = 3464 xx 9.8`
Also `R' = (u^2sin 2theta')/g => 5000 = (3464 xx 9.8 xx sin 2theta)/9.8`
i.e `sin 2theta' = 5000/3464 = 1.44`
Which is impossible because sine of an angle cannot be more than 1. Thus this target cannot be hoped to be hit.
APPEARS IN
RELATED QUESTIONS
Show that for a projectile the angle between the velocity and the x-axis as a function of time is given by
`theta(t) =tan^(-1) ((v_(0y) - "gt")/v_(o x))`
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s a part is 30°, what is the speed of the aircraft?
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
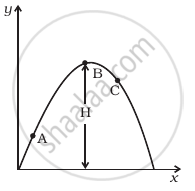
A particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure, where x and y indicate horizontal and vertical directions, respectively. Show in the diagram, direction of velocity and acceleration at points A, B and C.
A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At what angle of sight (w.r.t. horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?
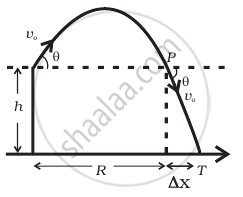
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
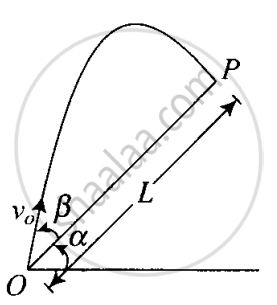
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
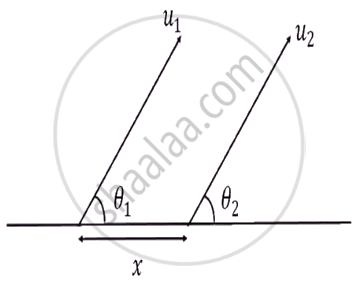
Two particles are projected simultaneously from the level ground as shown in figure. They may collide after a time:
If a baseball player can throw a ball at maximum distance = d over a ground, the maximum vertical height to which he can throw it, will be (Ball has same initial speed in each case):
A circular disc of radius r = 5m is rotating in horizontal plane about y-axis. Y-axis is vertical axis passing through the centre of disc and x-z is the horizontal plane at ground. The height of disc above ground is h = 5 m. Small particles are ejecting from disc in horizontal direction with speed 12 m/s from the circumference of disc then the distance of these particles from origin when they hits the x-z plane is:
