Advertisements
Advertisements
Question
A particle slides down a frictionless parabolic (y = x2) track (A – B – C) starting from rest at point A (Figure). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then
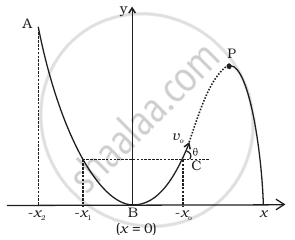
Options
KE at P = KE at B
height at P = height at A
total energy at P = total energy at A
time of travel from A to B = time of travel from B to P
Solution
Total energy at P = total energy at A
Explanation:
As the given track y = x2 is a frictionless track thus, the total energy (KE + PE) will be the same throughout the journey.
Hence, total energy at A = Total energy at P. At B, the particle is having only KE but at P some KE is converted to P.
Hence, (KE)B > (KE)P
Total energy at A = PE = Total energy at B = KE
= Total energy at P
= PE + KE
The potential energy at A is converted to KE and PE at P
Hence (PE)P < (PE)A
Hence, (Height)P < (Height)A
As Height of P < Height of A
Hence, path length AB > path length BP
Hence, the time of travel from A to B ≠ Time of travel from B to P.
APPEARS IN
RELATED QUESTIONS
A cricketer can throw a ball to a maximum horizontal distance of 100 m. How much high above the ground can the cricketer throw the same ball?
Show that for a projectile the angle between the velocity and the x-axis as a function of time is given by
`theta(t) =tan^(-1) ((v_(0y) - "gt")/v_(o x))`
Show that the projection angle `theta_o` for a projectile launched from the origin is given by
`theta_o =tan^(-1) ((4h_m)/R)`
Where the symbols have their usual meaning
A cricket ball thrown across a field is at heights h1 and h2 from the point of projection at times t1 and t2 respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is
The horizontal range of a projectile fired at an angle of 15° is 50 m. If it is fired with the same speed at an angle of 45°, its range will be ______.
A circular disc of radius r = 5m is rotating in horizontal plane about y-axis. Y-axis is vertical axis passing through the centre of disc and x-z is the horizontal plane at ground. The height of disc above ground is h = 5 m. Small particles are ejecting from disc in horizontal direction with speed 12 m/s from the circumference of disc then the distance of these particles from origin when they hits the x-z plane is:
For a projectile thrown into space with a speed v, the horizontal range is `(sqrt3"v"^2)/(2"g")`. The vertical range is `"v"^2/(8"g")`. The angle which the projectile makes with the horizontal initially is ______.
A person standing on a truck moving with a uniform velocity of 14.7 ms-1 on a horizontal road throws a ball in such a way that it returns to him after 4s. Find the speed and angle of projection as seen by a man on the road ______.
An object is projected in the air with initial velocity u at an angle θ. The projectile motion is such that the horizontal range R, is maximum.
Another object is projected in the air with a horizontal range half of the range of first object. The initial velocity remains same in both the case. The value of the angle of projection, at which the second object is projected, will be ______ degree.
A person throws a ball with a speed of 10 m/s at an angle of 30° with horizontally from the top of a 10 m high tower. The distance of the ball from the foot of the tower after falling on the ground will be ______.
