Advertisements
Advertisements
Question
The horizontal range of a projectile fired at an angle of 15° is 50 m. If it is fired with the same speed at an angle of 45°, its range will be ______.
Options
60 m
71 m
100 m
141 m
Solution
The horizontal range of a projectile fired at an angle of 15° is 50 m. If it is fired with the same speed at an angle of 45°, its range will be 100 m.
Explanation:
We know that
Where θ is angle of projection
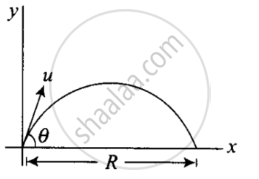
Given, θ = 15° and R = 50 m
Range, R = `(u^2 sin 2 θ)/g`
Putting all the given values in the formula, we get
⇒ R = `50 m = (u^2 sin(2 xx 15^circ))/g`
⇒ `50 xx g = u^2 sin 30^circ = u^2 xx 1/2`
⇒ `50 xx g xx 2 = u^2`
⇒ `u^2 = 50 xx 9.8 xx 2 = 100 xx 9.8` = 980
⇒ `u = sqrt(980)`
= `sqrt(49 xx 20)`
= `7 xx 2 xx sqrt(5)` m/s
= `14 xx 2.23` m/s
= 31.304 m/s
For θ = 45°, R = `(u^2 sin 2 xx 45^circ)/g = u^2/g` ......(∵ sin 90° = 1)
⇒ R = `(14sqrt(5))^2/g`
= `(14 xx 14 xx 5)/9.8`
= 100 m
APPEARS IN
RELATED QUESTIONS
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s a part is 30°, what is the speed of the aircraft?
A cricket ball thrown across a field is at heights h1 and h2 from the point of projection at times t1 and t2 respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
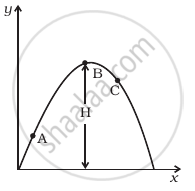
A particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure, where x and y indicate horizontal and vertical directions, respectively. Show in the diagram, direction of velocity and acceleration at points A, B and C.
A ball is thrown from a roof top at an angle of 45° above the horizontal. It hits the ground a few seconds later. At what point during its motion, does the ball have
- greatest speed.
- smallest speed.
- greatest acceleration?
Explain
A boy travelling in an open car moving on a levelled road with constant speed tosses a ball vertically up in the air and catches it back. Sketch the motion of the ball as observed by a boy standing on the footpath. Give explanation to support your diagram.
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
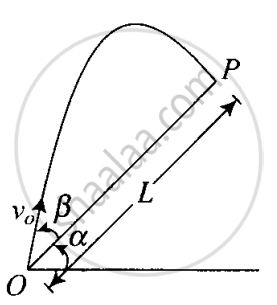
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
If T be the total time of flight of a current of water and H be the maximum height attained by it from the point of projection, then HIT will be : (u = projection velocity, e = projection angle)
Two stones are projected with the same speed but making different angles with the horizontal. Their ranges are equal. If the angle of projection of one is `pi/3` and its maximum height is y1 then the maximum height of the other will be ______.
