Advertisements
Advertisements
प्रश्न
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s a part is 30°, what is the speed of the aircraft?
उत्तर
The positions of the observer and the aircraft are shown in the given figure.
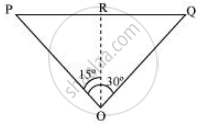
Height of the aircraft from ground, OR = 3400 m
Angle subtended between the positions, ∠POQ = 30°
Time = 10 s
In ΔPRO:
`tan 15^@ =(PR)/(OR)`
`"PR" = "OR" tan 15^@`
`=3400 xx tan 15^@`
`= 3400 xx 0.2679 = 910.86`
ΔPRO is similar to ΔRQO.
∴PR = RQ
PQ = PR + RQ
= 2PR
= 2 × 910.86 = 1821.72 m
∴ Speed of aircraft = `1821.72/10 = 182.2 "m/s"`
APPEARS IN
संबंधित प्रश्न
Show that the projection angle `theta_o` for a projectile launched from the origin is given by
`theta_o =tan^(-1) ((4h_m)/R)`
Where the symbols have their usual meaning
A cricket ball thrown across a field is at heights h1 and h2 from the point of projection at times t1 and t2 respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is
A ball rolls of the top of the stairway with a horizontal velocity u ms−1. If the steps are h m high and b m wide, the ball will hit the edge of the nth step, if:
Two particles are projected in air with speed vo at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices
- Angle of projection: q1 > q2
- Time of flight: T1 > T2
- Horizontal range: R1 > R2
- Total energy: U1 > U2
A football is kicked into the air vertically upwards. What is its acceleration?
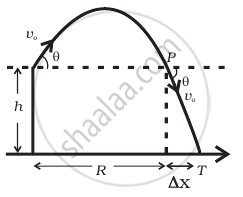
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
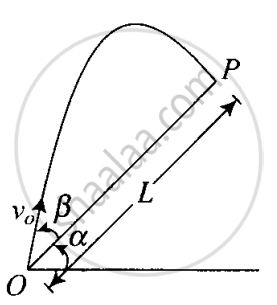
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
If a baseball player can throw a ball at maximum distance = d over a ground, the maximum vertical height to which he can throw it, will be (Ball has same initial speed in each case):
The minimum speed in m/s with which a projectile must be thrown from origin at ground so that it is able to pass through a point P (30 m, 40 m) is ______. (g = 10 m/s2)
For a projectile thrown into space with a speed v, the horizontal range is `(sqrt3"v"^2)/(2"g")`. The vertical range is `"v"^2/(8"g")`. The angle which the projectile makes with the horizontal initially is ______.
