Advertisements
Advertisements
प्रश्न
Two particles are projected in air with speed vo at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices
- Angle of projection: q1 > q2
- Time of flight: T1 > T2
- Horizontal range: R1 > R2
- Total energy: U1 > U2
उत्तर
a and b
Explanation:
According to formula, Max height of a projectile is
H = `(u^2 sin^2 theta)/(2g)`
a. `H_1 > H_2`
`sin^2 theta_1 > sin^2 theta_2`
`(sin theta_1 + sin theta_2) (sin theta_1 - sin theta_2) > 0`
So, `(sin theta_1 + sin theta_2) > 0` or `(sin theta_1 - sin theta_2) > 0`
So, `θ_1 > θ_2` and θ lies between 0 and 90 degree i.e. acute
b. `T_1/T_2 = sin theta_1/sin theta_2`
`T_1/T_2 = sin theta_1/sin theta_2`
`T_1 sin theta_2 = T_2 sin theta_1`
Since sin θ1 > sin θ2
T1 > T2
Important points about the time of flight: For complementary angles of projection θ and 90° – θ.
a. Ratio of time flight = `T_1/T_2`
= `(2 u sin theta/g)/(2u sin (90^circ - theta)/g)`
= tan θ
⇒ `T_1/T_2` = tan θ
b. Multiplication of time of flight = `T_1T_2`
= `(2u sin theta)/g (2u cos theta)/g`
⇒ `T_1T_2 = (2R)/g`
APPEARS IN
संबंधित प्रश्न
The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 m s–1 can go without hitting the ceiling of the hall?
A body of mass m is projected horizontally with a velocity v from the top of a tower of height h and it reaches the ground at a distance x from the foot of the tower. If the second body of mass of 4 m is projected horizontally from the top of a tower of the height of 4 h, it reaches the ground at a distance of 4x from the foot of the tower. The horizontal velocity of the second body is:
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
A boy throws a ball in air at 60° to the horizontal along a road with a speed of 10 m/s (36 km/h). Another boy sitting in a passing by car observes the ball. Sketch the motion of the ball as observed by the boy in the car, if car has a speed of (18 km/h). Give explanation to support your diagram.
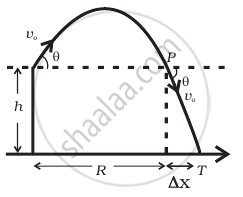
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
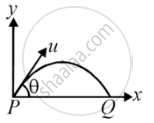
Average torque on a projectile of mass m, initial speed u and angle of projection θ between initial and final positions P and Q as shown in figure about the point of projection is ______.
A person standing on a truck moving with a uniform velocity of 14.7 ms-1 on a horizontal road throws a ball in such a way that it returns to him after 4s. Find the speed and angle of projection as seen by a man on the road ______.
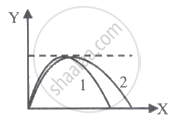
The trajectories of the two projectiles are shown in the figure. Let T1 and T2 be the time periods and u1 and u2 be their speeds of projection. Then ______.
An object is projected in the air with initial velocity u at an angle θ. The projectile motion is such that the horizontal range R, is maximum.
Another object is projected in the air with a horizontal range half of the range of first object. The initial velocity remains same in both the case. The value of the angle of projection, at which the second object is projected, will be ______ degree.
The initial speed of a bullet fired from a rifle is 630 m/s. The rifle is fired at the centre of a target 700 m away at the same level as the target. How far above the centre of the target the rifle must be aimed in order to hit the target?
