Advertisements
Advertisements
प्रश्न
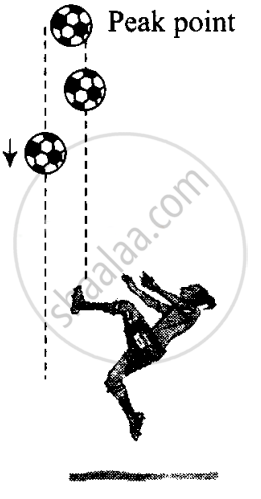
A football is kicked into the air vertically upwards. What is its acceleration?
उत्तर
The situation is shown in the diagram below in which a football is kicked into the air vertically upwards. Acceleration of the football will always be vertical downward and is called acceleration due to gravity (g).
APPEARS IN
संबंधित प्रश्न
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to the fixed, and neglect air resistance.
Two particles are projected in air with speed vo at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices
- Angle of projection: q1 > q2
- Time of flight: T1 > T2
- Horizontal range: R1 > R2
- Total energy: U1 > U2
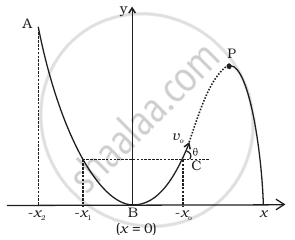
A particle slides down a frictionless parabolic (y = x2) track (A – B – C) starting from rest at point A (Figure). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then
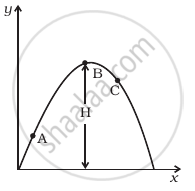
A particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure, where x and y indicate horizontal and vertical directions, respectively. Show in the diagram, direction of velocity and acceleration at points A, B and C.
A ball is thrown from a roof top at an angle of 45° above the horizontal. It hits the ground a few seconds later. At what point during its motion, does the ball have
- greatest speed.
- smallest speed.
- greatest acceleration?
Explain
A boy throws a ball in air at 60° to the horizontal along a road with a speed of 10 m/s (36 km/h). Another boy sitting in a passing by car observes the ball. Sketch the motion of the ball as observed by the boy in the car, if car has a speed of (18 km/h). Give explanation to support your diagram.
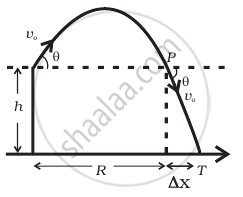
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
Two particles are projected simultaneously from the level ground as shown in figure. They may collide after a time:
Two stones are projected with the same speed but making different angles with the horizontal. Their ranges are equal. If the angle of projection of one is `pi/3` and its maximum height is y1 then the maximum height of the other will be ______.
An object is projected in the air with initial velocity u at an angle θ. The projectile motion is such that the horizontal range R, is maximum.
Another object is projected in the air with a horizontal range half of the range of first object. The initial velocity remains same in both the case. The value of the angle of projection, at which the second object is projected, will be ______ degree.
