Advertisements
Advertisements
प्रश्न
A five-digit number AABAA is divisible by 33. Write all the numbers of this form.
उत्तर
Given, a number of the form AABAA is divisible by 33.
Then, it is also divisible by 3 and 11, as if a number a is divisible by b, then it is also divisible by each factor of b.
Since, AABAA is divisible by 3, sum its digits is also divisible by 3.
i.e. 4 + 4 + 8 + A + 4 = 0, 3, 6, 9 ...
or 4/4 + 8 = 0, 3, 6, 9, ...(i)
From equation (i), we have
Further, the given number is also divisible by 11,
Therefore (2/4 + 8) – 2A = 0, 11, 22, ...
B = Q 11, 22, ...
8 = 0 ...[8 is a digit of the given number]
4/4 = 12 or 24 or 36 A = 3, 6, 9
Hence, the required numbers are 33033, 66066 and 99099.
APPEARS IN
संबंधित प्रश्न
Without performing actual addition and division write the quotient when the sum of 69 and 96 is divided by
(i) 11
(ii) 15
Given an example of a number which is divisible by 3 but not by 6.
Look at the patterns of numbers in hexagons.
Each side has 2 circles and 1 box.
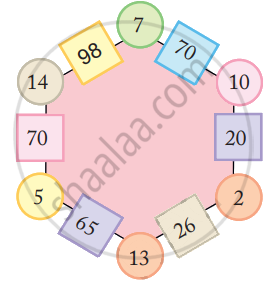
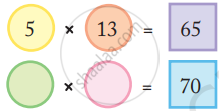
- Look at the number 65 in the box. Which are the circles next to it?
- Can you see how the rule works?
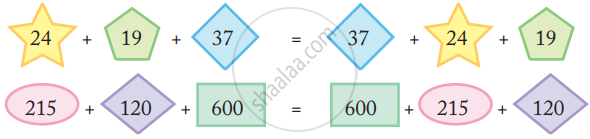
Are they equal?
Fill in the blank space in the same way.

If 6A × B = A 8 B, then the value of A – B is ______.
20 × 3 is a multiple of 3 if the digit × is ______ or ______ or ______.
If the digit 1 is placed after a 2-digit number whose tens is t and ones digit is u, the new number is ______.
Find the value of k where 31k2 is divisible by 6.
If 148101B095 is divisible by 33, find the value of B.
