Advertisements
Advertisements
प्रश्न
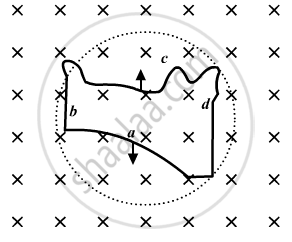
A flexible wire of irregular shape, abcd, as shown in the figure, turns into a circular shape when placed in a region of magnetic field which is directed normal to the plane of the loop away from the reader. Predict the direction of the induced current in the wire.
उत्तर
The wire is expanding to form a circle, which means that force is acting outwards on each part of the wire because of the magnetic field (acting in the downwards direction). The direction of the induced current should be such that it will produce magnetic field in upward direction (towards the reader). Hence, the force on the wire will be towards inward direction, i.e., induced current is flowing in anticlockwise direction in the loop from c-b-a-d-c.
APPEARS IN
संबंधित प्रश्न
An electron moving horizontally with a velocity of 4 ✕ 104 m/s enters a region of uniform magnetic field of 10−5 T acting vertically upward as shown in the figure. Draw its trajectory and find out the time it takes to come out of the region of magnetic
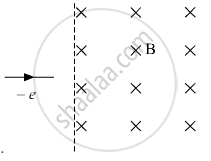
field.
A proton and a deuteron having equal momenta enter in a region of a uniform magnetic field at right angle to the direction of a the field. Depict their trajectories in the field.
A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one point. If a magnetic field is switched on in the vertical direction, the tension in the string
If a charged particle projected in a gravity-free room deflects,
(a) there must be an electric field
(b) there must be a magnetic field
(c) both fields cannot be zero
(d) both fields can be non-zero
Using the formula \[\vec{F} = q \vec{v} \times \vec{B} \text{ and } B = \frac{\mu_0 i}{2\pi r}\]show that the SI units of the magnetic field B and the permeability constant µ0 may be written as N mA−1 and NA−2 respectively.
A wire, carrying a current i, is kept in the x−y plane along the curve y = A sin `((2x)/lamda x)`. magnetic field B exists in the z direction. Find the magnitude of the magnetic force on the portion of the wire between x = 0 and x = λ.
Consider a non-conducting ring of radius r and mass m that has a total charge qdistributed uniformly on it. The ring is rotated about its axis with an angular speed ω. (a) Find the equivalent electric current in the ring. (b) Find the magnetic moment µ of the ring. (c) Show that `pi = (q)/(2m)` l, where l is the angular momentum of the ring about its axis of rotation.
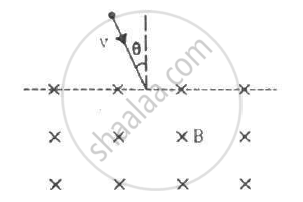
A particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B, as shown in the figure. (a) Find the radius of the circular arc it describes in the magnetic field. (b) Find the angle subtended by the arc at the centre. (c) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.
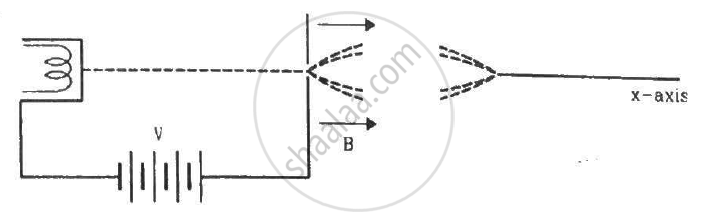
Electrons emitted with negligible speed from an electron gun are accelerated through a potential difference V along the x-axis. These electrons emerge from a narrow hole into a uniform magnetic field B directed along this axis. However, some of the electrons emerging from the hole make slightly divergent angles, as shown in the figure. Show that these paraxial electrons are refocussed on the x-axis at a distance `sqrt(8pi^2mV)/(eB^2).`
Current flows through uniform, square frames as shown in the figure. In which case is the magnetic field at the centre of the frame not zero?
