Advertisements
Advertisements
प्रश्न
Using the formula \[\vec{F} = q \vec{v} \times \vec{B} \text{ and } B = \frac{\mu_0 i}{2\pi r}\]show that the SI units of the magnetic field B and the permeability constant µ0 may be written as N mA−1 and NA−2 respectively.
उत्तर
Using the relation \[\vec{F} = q v^\rightharpoonup \times \vec{B}\] , we get
\[ = \frac{F}{Itv}\]
Force (F) = N
Current (I) = A
Time (T) = s
Velocity (v) = m/s
APPEARS IN
संबंधित प्रश्न
Show that the kinetic energy of the particle moving in a magnetic field remains constant.
A proton and an α-particle move perpendicular to a magnetic field. Find the ratio of radii of circular paths described by them when both have (i) equal velocities, and (ii) equal kinetic energy.
An electron moving horizontally with a velocity of 4 ✕ 104 m/s enters a region of uniform magnetic field of 10−5 T acting vertically upward as shown in the figure. Draw its trajectory and find out the time it takes to come out of the region of magnetic
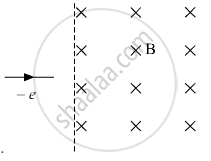
field.
A straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid air by a uniform magnetic field B. What is the magnitude of the magnetic field?
Assume that the magnetic field is uniform in a cubical region and zero outside. Can you project a charged particle from outside into the field, so that the particle describes a complete circle in the field?
A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one point. If a magnetic field is switched on in the vertical direction, the tension in the string
A beam consisting of protons and electrons moving at the same speed goes through a thin region in which there is a magnetic field perpendicular to the beam. The protons and the electrons
Two ions have equal masses but one is singly-ionised and the other is doubly-ionised. They are projected from the same place in a uniform magnetic field with the same velocity perpendicular to the field.
(a) Both ions will move along circles of equal radii.
(b) The circle described by the singly-ionised charge will have a radius that is double that of the other circle.
(c) The two circles do not touch each other.
(d) The two circles touch each other.
Consider three quantities \[x = E/B, y = \sqrt{1/ \mu_0 \epsilon_0}\] and \[z = \frac{l}{CR}\] . Here, l is the length of a wire, C is a capacitance and R is a resistance. All other symbols have standard meanings.
(a) x, y have the same dimensions.
(b) y, z have the same dimensions.
(c) z, x have the same dimensions.
(d) None of the three pairs have the same dimensions.
A 10 g bullet with a charge of 4.00 μC is fired at a speed of 270 m s−1 in a horizontal direction. A vertical magnetic field of 500 µT exists in the space. Find the deflection of the bullet due to the magnetic field as it travels through 100 m. Make appropriate approximations.
A current of 2 A enters at the corner d of a square frame abcd of side 20 cm and leaves at the opposite corner b. A magnetic field B = 0.1 T exists in the space in a direction perpendicular to the plane of the frame, as shown in the figure. Find the magnitude and direction of the magnetic forces on the four sides of the frame.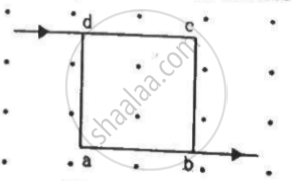
Prove that the force acting on a current-carrying wire, joining two fixed points a and b in a uniform magnetic field, is independent of the shape of the wire.
A semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
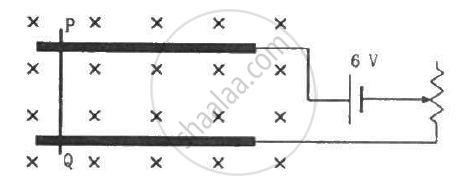
A metal wire PQ of mass 10 g lies at rest on two horizontal metal rails separated by 4.90 cm (figure). A vertically-downward magnetic field of magnitude 0.800 T exists in the space. The resistance of the circuit is slowly decreased and it is found that when the resistance goes below 20.0 Ω, the wire PQ starts sliding on the rails. Find the coefficient of friction.
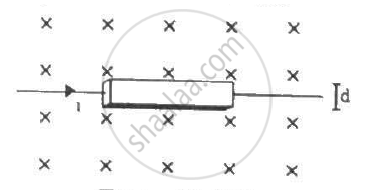
A current i is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n. (a) Find the drift velocity v of the electrons. (b) If a magnetic field B exists in the region, as shown in the figure, what is the average magnetic force on the free electrons? (c) Due to the magnetic force, the free electrons get accumulated on one side of the conductor along its length. This produces a transverse electric field in the conductor, which opposes the magnetic force on the electrons. Find the magnitude of the electric field which will stop further accumulation of electrons. (d) What will be the potential difference developed across the width of the conductor due to the electron-accumulation? The appearance of a transverse emf, when a current-carrying wire is placed in a magnetic field, is called Hall effect.
Protons with kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field, so that it just misses a plane target kept at a distance l in front of the accelerator. Find the magnetic field.
A proton is projected with a velocity of 3 × 106 m s−1 perpendicular to a uniform magnetic field of 0.6 T. Find the acceleration of the proton.
The figure shows a convex lens of focal length 12 cm lying in a uniform magnetic field Bof magnitude 1.2 T parallel to its principal axis. A particle with charge 2.0 × 10−3 C and mass 2.0 × 10−5 kg is projected perpendicular to the plane of the diagram with a speed of 4.8 m s−1. The particle moves along a circle with its centre on the principal axis at a distance of 18 cm from the lens. Show that the image of the particle moves along a circle and find the radius of that circle.

When does a moving charged particle nor experience any force while moving through a uniform magnetic field?
