Advertisements
Advertisements
प्रश्न
A current of 10 A is established in a long wire along the positive z-axis. Find the magnetic field \[\vec{B}\] at the point (1 m, 0, 0).
उत्तर
Given:
Magnitude of current, I = 10 A
Separation of the point from the wire, d = 1 m
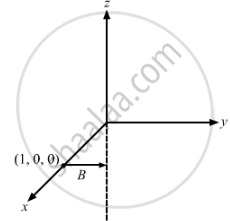
The magnetic field \[\vec{B}\] at point (1 m, 0, 0) is given by
\[B = \frac{\mu_0 i}{2\pi d} = \frac{4\pi \times {10}^{- 7} \times 10}{2\pi \times 1}\]
\[ \Rightarrow B = 2 \times {10}^{- 6} T\]
(Along the +ve y-axis by the right-hand thumb rule)
APPEARS IN
संबंधित प्रश्न
Using the concept of force between two infinitely long parallel current carrying conductors, define one ampere of current.
How does one understand this motional emf by invoking the Lorentz force acting on the free charge carriers of the conductor? Explain.
Derive the expression for force per unit length between two long straight parallel current carrying conductors. Hence define one ampere.
An electron beam projected along the positive x-axis deflects along the positive y-axis. If this deflection is caused by a magnetic field, what is the direction of the field? Can we conclude that the field is parallel to the z-axis?
and ```vecE` and `vecB`denote electric and magnetic fields in a frame S and `vecE`→ and `vecB` in another frame S' moving with respect to S at a velocity `vecV` Two of the following equations are wrong. Identify them.
(a) `B_y^, = B_y + (vE_z)/c^2`
(b) `E_y^' = E_y - (vB_z)/(c^2)`
`(c) Ey = By + vE_z`
`(d) E_y = E_y + vB_z`
Two parallel, long wires carry currents i1 and i2 with i1 > i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 µT. If the direction of i2 is reversed, the field becomes 30 µT. The ratio i1/i2 is
A transmission wire carries a current of 100 A. What would be the magnetic field B at a point on the road if the wire is 8 m above the road?
A long, straight wire carrying a current of 1.0 A is placed horizontally in a uniform magnetic field B = 1.0 × 10−5 T pointing vertically upward figure. Find the magnitude of the resultant magnetic field at the points P and Q, both situated at a distance of 2.0 cm from the wire in the same horizontal plane.
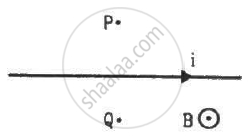
A long, straight wire of radius r carries a current i and is placed horizontally in a uniform magnetic field B pointing vertically upward. The current is uniformly distributed over its cross section. (a) At what points will the resultant magnetic field have maximum magnitude? What will be the maximum magnitude? (b) What will be the minimum magnitude of the resultant magnetic field?
Figure shows a metallic wire of resistance 0.20 Ω sliding on a horizontal, U-shaped metallic rail. The separation between the parallel arms is 20 cm. An electric current of 2.0 µA passes through the wire when it is slid at a rate of 20 cm s−1. If the horizontal component of the earth's magnetic field is 3.0 × 10−5 T, calculate the dip at the place.
Figure shows two parallel wires separated by a distance of 4.0 cm and carrying equal currents of 10 A along opposite directions. Find the magnitude of the magnetic field B at the points A1, A2, A3.

Two long, straight wires, each carrying a current of 5 A, are placed along the x- and y-axis respectively. The currents point along the positive directions of the axes. Find the magnetic fields at the points (a) (1 m, 1 m), (b) (−1 m, 1 m), (c) (−1 m, −1 m) and (d) (1 m, −1 m).
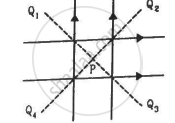
Four long, straight wires, each carrying a current of 5.0 A, are placed in a plane as shown in figure. The points of intersection form a square of side 5.0 cm.
(a) Find the magnetic field at the centre P of the square.
(b) Q1, Q2, Q3, and Q4, are points situated on the diagonals of the square and at a distance from P that is equal to the diagonal of the square. Find the magnetic fields at these points.
Consider a 10-cm long piece of a wire which carries a current of 10 A. Find the magnitude of the magnetic field due to the piece at a point which makes an equilateral triangle with the ends of the piece.
Two parallel wires separated by a distance of 10 cm carry currents of 10 A and 40 A along the same direction. Where should a third current by placed so that it experiences no magnetic force?
A milli voltmeter of 25 milli volt range is to be converted into an ammeter of 25 ampere range. The value (in ohm) of necessary shunt will be ______.
The nature of parallel and anti-parallel currents are ______.
Do magnetic forces obey Newton’s third law. Verify for two current elements dl1 = dlî located at the origin and dl2 = dlĵ located at (0, R, 0). Both carry current I.
