Advertisements
Advertisements
प्रश्न
Using the concept of force between two infinitely long parallel current carrying conductors, define one ampere of current.
उत्तर
One ampere of current can be defined as the amount of current which when flowing (in same direction) through two infinitely long parallel wires separated by one metre produces an attractive force of 2 × 10−7 N/m. The wires must have negligible circular cross-section and they must be placed in vacuum.
APPEARS IN
संबंधित प्रश्न
How does one understand this motional emf by invoking the Lorentz force acting on the free charge carriers of the conductor? Explain.
Two long and parallel straight wires A and B carrying currents of 8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.
Two long straight parallel conductors 'a' and 'b', carrying steady currents Ia and Ib are separated by a distance d. Write the magnitude and direction of the magnetic field produced by the conductor 'a' at the points along the conductor 'b'. If the currents are flowing in the same direction, what is the nature and magnitude of the force between the two conductors?
and ```vecE` and `vecB`denote electric and magnetic fields in a frame S and `vecE`→ and `vecB` in another frame S' moving with respect to S at a velocity `vecV` Two of the following equations are wrong. Identify them.
(a) `B_y^, = B_y + (vE_z)/c^2`
(b) `E_y^' = E_y - (vB_z)/(c^2)`
`(c) Ey = By + vE_z`
`(d) E_y = E_y + vB_z`
An electron is moving along the positive x-axis. You want to apply a magnetic field for a short time so that the electron may reverse its direction and move parallel to the negative x-axis. This can be done by applying the magnetic field along
(a) y-axis
(b) z-axis
(c) y-axis only
(d) z-axis only
A hypothetical magnetic field existing in a region is given by `vecB = B_0 vece` where `vece`_r denotes the unit vector along the radial direction. A circular loop of radius a, carrying a current i, is placed with its plane parallel to the x−y plane and the centre at (0, 0, d). Find the magnitude of the magnetic force acting on the loop.
A straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is µ. If the wire carries a current i, what minimum magnetic field should exist in the space in order to slide the wire on the rails?
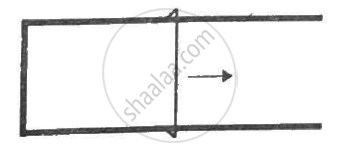
Figure shows a metallic wire of resistance 0.20 Ω sliding on a horizontal, U-shaped metallic rail. The separation between the parallel arms is 20 cm. An electric current of 2.0 µA passes through the wire when it is slid at a rate of 20 cm s−1. If the horizontal component of the earth's magnetic field is 3.0 × 10−5 T, calculate the dip at the place.
Three coplanar parallel wires, each carrying a current of 10 A along the same direction, are placed with a separation 5.0 cm between the consecutive ones. Find the magnitude of the magnetic force per unit length acting on the wires.
Equal currents are passing through two very long and straight parallel wires in the same direction. They will ______
