Advertisements
Advertisements
प्रश्न
Two ions have equal masses but one is singly-ionised and the other is doubly-ionised. They are projected from the same place in a uniform magnetic field with the same velocity perpendicular to the field.
(a) Both ions will move along circles of equal radii.
(b) The circle described by the singly-ionised charge will have a radius that is double that of the other circle.
(c) The two circles do not touch each other.
(d) The two circles touch each other.
उत्तर
(b) The circle described by the singly-ionised charge will have a radius that is double that of the other circle.
(d) The two circles touch each other.
The radius of the orbit of a charged particle in an external magnetic field,
`r = (mV)/(qB)`
where r is the radius of the circle, m is the mass of the ion, V is the velocity with which the ion is projected, q is the charge on the ion and B is the uniform magnetic field.
Since the mass m, the velocity V and the magnetic field B are same for both the ions, r is inversely proportional to the charge on the ion.
Hence, the radius of the circle described by the singly-charged ion will be twice the radius of the circle described by doubly-ionised ion.
Moreover, as both the charges are projected from the same place, the two circles described by them will touch each other at the point of projection.
APPEARS IN
संबंधित प्रश्न
Write the expression, in a vector form, for the Lorentz magnetic force \[\vec{F}\] due to a charge moving with velocity \[\vec{V}\] in a magnetic field \[\vec{B}\]. What is the direction of the magnetic force?
Write the expression for the force `vecF` acting on a particle of mass m and charge q moving with velocity `vecV` in a magnetic field `vecB` , Under what conditions will it move in (i) a circular path and (ii) a helical path?
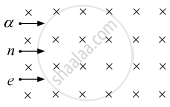
A neutron, an electron and an alpha particle, moving with equal velocities, enter a uniform magnetic field going into the plane of the paper, as shown. Trace their paths in the field and justify your answer.
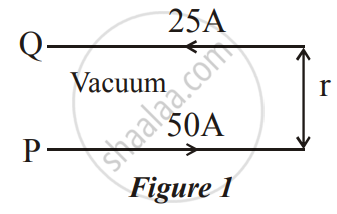
A long horizontal wire P carries a current of 50A. It is rigidly fixed. Another wire Q is placed directly above and parallel to P, as shown in Figure 1 below. The weight per unit length of the wire Q is 0.025 Nm-1 and it carries a current of 25A. Find the distance 'r' of the wire Q from the wire P so that the wire Q remains at rest
An electron moving horizontally with a velocity of 4 ✕ 104 m/s enters a region of uniform magnetic field of 10−5 T acting vertically upward as shown in the figure. Draw its trajectory and find out the time it takes to come out of the region of magnetic
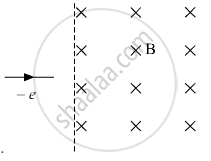
field.
A straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid air by a uniform magnetic field B. What is the magnitude of the magnetic field?
Assume that the magnetic field is uniform in a cubical region and zero outside. Can you project a charged particle from outside into the field, so that the particle describes a complete circle in the field?
An electric current i enters and leaves a uniform circular wire of radius a through diametrically opposite points. A charged particle q, moving along the axis of the circular wire, passes through its centre at speed v. The magnetic force acting on the particle, when it passes through the centre, has a magnitude equal to
A charged particle moves along a circle under the action of possible constant electric and magnetic fields. Which of the following is possible?
(a) E = 0, B = 0
(b) E = 0, B ≠ 0
(c) E ≠ 0, B = 0
(d) E ≠ 0, B ≠ 0
If a charged particle moves unaccelerated in a region containing electric and magnetic fields
(a) `vecE "must be perpendicular" to vecB`
(b) `vecv "must be perpendicular" to vecE`
(c) must be perpendicular to v_B
A particle is projected in a plane perpendicular to a uniform magnetic field. The area bounded by the path described by the particle is proportional to
Two particles X and Y having equal charge, after being accelerated through the same potential difference enter a region of uniform magnetic field and describe circular paths of radii R1 and R2 respectively. The ratio of the mass of X to that of Y is ______.
When a proton is released from rest in a room, it starts with an initial acceleration a0towards west. When it is projected towards north with a speed v0, it moves with an initial acceleration 3a0 towards west. Find the electric field and the maximum possible magnetic field in the room.
A particle of charge 2.0 × 10−8 C and mass 2.0 × 10−10 g is projected with a speed of 2.0 × 103 m s−1 in a region with a uniform magnetic field of 0.10 T. The velocity is perpendicular to the field. Find the radius of the circle formed by the particle and also the time period.
Protons with kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field, so that it just misses a plane target kept at a distance l in front of the accelerator. Find the magnetic field.
A square coil of edge l and with n turns carries a current i. It is kept on a smooth horizontal plate. A uniform magnetic field B exists parallel to an edge. The total mass of the coil is M. What should be the minimum value of B for which the coil will start tipping over?
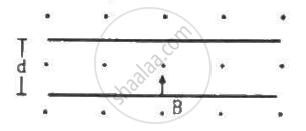
A particle of mass m and charge q is projected into a region that has a perpendicular magnetic field B. Find the angle of deviation (figure) of the particle as it comes out of the magnetic field if the width d of the region is very slightly smaller than
(a) `(mv)/(qB)` (b)`(mv)/(2qB)` (c)`(2mv)/(qB)`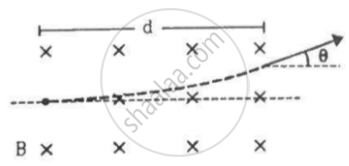
Doubly-ionised helium ions are projected with a speed of 10 km s−1 in a direction perpendicular to a uniform magnetic field of magnitude 1.0 T. Find (a) the force acting on an ion (b) the radius of the circle in which it circulates and (c) the time taken by an ion to complete the circle.
An electron is emitted with negligible speed from the negative plate of a parallel-plate capacitor charged to a potential difference V. The separation between the plates is dand a magnetic field B exists in the space, as shown in the figure. Show that the electron will fail to strike the upper plates if `d > ((2m_eV)/(eB_0^2))^(1/2)`