Advertisements
Advertisements
प्रश्न
A square coil of edge l and with n turns carries a current i. It is kept on a smooth horizontal plate. A uniform magnetic field B exists parallel to an edge. The total mass of the coil is M. What should be the minimum value of B for which the coil will start tipping over?
उत्तर
Given:
Number of turns in the coil = n
Edge of the square loop = l
Magnetic field intensity = B
Magnitude of current = i
Angle between area vector and magnetic field, θ = 90°
Torque acting on the coil due to magnetic field,
τ = niABsinθ
Here, A is the area of the coil.
`τ = n"if"Bsin90^circ`
Torque produced due to weight, τweight =
`(mgl)/2`
For the coil to start tipping over,
τ ≥ τweight
For minimum value of B,
τ = τweight
`⇒ nil^2B =(mg)/l`
`⇒ B = (MG)/(2nil)`
APPEARS IN
संबंधित प्रश्न
An electron moving horizontally with a velocity of 4 ✕ 104 m/s enters a region of uniform magnetic field of 10−5 T acting vertically upward as shown in the figure. Draw its trajectory and find out the time it takes to come out of the region of magnetic
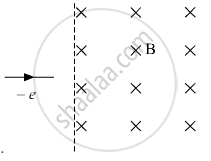
field.
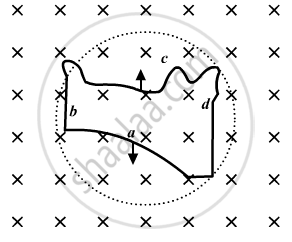
A flexible wire of irregular shape, abcd, as shown in the figure, turns into a circular shape when placed in a region of magnetic field which is directed normal to the plane of the loop away from the reader. Predict the direction of the induced current in the wire.
A proton and a deuteron having equal momenta enter in a region of a uniform magnetic field at right angle to the direction of a the field. Depict their trajectories in the field.
Write the expression for Lorentz magnetic force on a particle of charge ‘q’ moving with velocity `vecv` in a magnetic field`vecB`. Show that no work is done by this force on the charged particle.
A positively-charged particle projected towards east is deflected towards north by a magnetic field. The field may be
A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one point. If a magnetic field is switched on in the vertical direction, the tension in the string
A beam consisting of protons and electrons moving at the same speed goes through a thin region in which there is a magnetic field perpendicular to the beam. The protons and the electrons
A charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
If a charged particle moves unaccelerated in a region containing electric and magnetic fields
(a) `vecE "must be perpendicular" to vecB`
(b) `vecv "must be perpendicular" to vecE`
(c) must be perpendicular to v_B
A magnetic field of \[(4.0\times10^-3 \overrightarrow k)\] T exerts a force of \[(4.0 \overrightarrow i + 3.0 \overrightarrow j ) \times 10^{−10} N\] on a particle with a charge of 1.0 × 10−9 C and going in the x − y plane. Find the velocity of the particle.
A magnetic field of strength 1.0 T is produced by a strong electromagnet in a cylindrical region of radius 4.0 cm, as shown in the figure. A wire, carrying a current of 2.0 A, is placed perpendicular to and intersecting the axis of the cylindrical region. Find the magnitude of the force acting on the wire.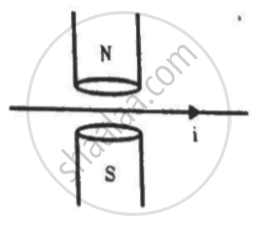
A semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
A wire, carrying a current i, is kept in the x−y plane along the curve y = A sin `((2x)/lamda x)`. magnetic field B exists in the z direction. Find the magnitude of the magnetic force on the portion of the wire between x = 0 and x = λ.
A circular coil of radius 2.0 cm has 500 turns and carries a current of 1.0 A. Its axis makes an angle of 30° with the uniform magnetic field of magnitude 0.40 T that exists in the space. Find the torque acting on the coil.
A narrow beam of singly-charged carbon ions, moving at a constant velocity of 6.0 × 104m s−1, is sent perpendicularly in a rectangular region of uniform magnetic field B = 0.5 T (figure). It is found that two beams emerge from the field in the backward direction, the separations from the incident beam being 3.0 cm and 3.5 cm. Identify the isotopes present in the ion beam. Take the mass of an ion = A(1.6 × 10−27) kg, where A is the mass number.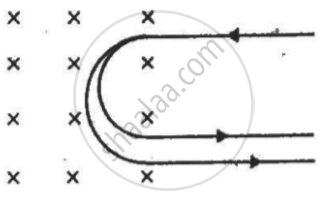
A particle of mass m and charge q is released from the origin in a region in which the electric field and magnetic field are given by
`vecB = -B_0 vecj and vecE = E_0 vecK `
Find the speed of the particle as a function of its z-coordinate.
When does a moving charged particle nor experience any force while moving through a uniform magnetic field?
A uniform magnetic field of 1.5 T exists in a cylindrical region of radius 10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if,
(a) the wire intersects the axis,
(b) the wire is turned from N-S to northeast-northwest direction,
(c) the wire in the N-S direction is lowered from the axis by a distance of 6.0 cm?
The velocity of a body of mass 2 kg as a function of time t is given by v(t) = 2t`hat"i" + "t"^2hat"j"`. The force acting on it, at time t = 2 s is given by ______.
