Advertisements
Advertisements
प्रश्न
A narrow beam of singly-charged carbon ions, moving at a constant velocity of 6.0 × 104m s−1, is sent perpendicularly in a rectangular region of uniform magnetic field B = 0.5 T (figure). It is found that two beams emerge from the field in the backward direction, the separations from the incident beam being 3.0 cm and 3.5 cm. Identify the isotopes present in the ion beam. Take the mass of an ion = A(1.6 × 10−27) kg, where A is the mass number.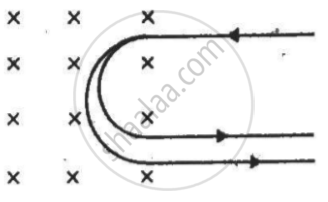
उत्तर
Given:
Velocity of a narrow beam of singly-charged carbon ions, v = 6.0 × 104 m s−1
Strength of magnetic field B = 0.5 T
Separations between the two beams from the incident beam are 3.0 cm and 3.5 cm.
Mass of an ion = A(1.6 × 10−27) kg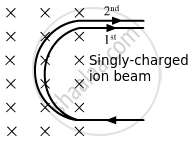
The radius of the curved path taken by the first beam, r_1 = `(m_1v)/(qB)`
where m1 is the mass of the first isotope and q is the charge.
For the second beam:
`r_2 = (m_2v)/(qB)`
where m2 is the mass of the first isotope and q is the charge.
`(r_1)/(r_2) =(m_1)/(qB)`
`(3//2)/(3.5//2) =
(A_1xx1.6xx10^-27)/(A_2xx1.6xx10^-27)`
`6/7 = (A_1)/(A_2)`
As
`r_1 = (m_1v)/(qB)`
⇒ `m_1 = (q_Br_1)/v`
⇒ `(1.6xx10^-19xx0.5xx0.015)/(6xx10^-27)`
= 20 × 10-27 kg
= `(20xx10^-27)/(1.6xx10^-27)u`
= 12.5 u
Also
`A_2 = 7/6A_1`
=` 7/6 xx 12.5`
= 14.58 u
So, the two isotopes of carbon used are 12C6 and 14C6.
APPEARS IN
संबंधित प्रश्न
Write the expression for the force `vecF` acting on a particle of mass m and charge q moving with velocity `vecV` in a magnetic field `vecB` , Under what conditions will it move in (i) a circular path and (ii) a helical path?
An electron moving horizontally with a velocity of 4 ✕ 104 m/s enters a region of uniform magnetic field of 10−5 T acting vertically upward as shown in the figure. Draw its trajectory and find out the time it takes to come out of the region of magnetic
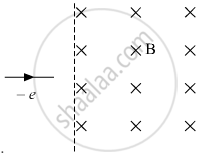
field.
A straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid air by a uniform magnetic field B. What is the magnitude of the magnetic field?
Write the expression for the force,`vecF` acting on a charged particle of charge ‘q’, moving with a velocity `vecV` in the presence of both electric field `vecF`and magnetic field `vecB` . Obtain the condition under which the particle moves undeflected through the fields.
A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one point. If a magnetic field is switched on in the vertical direction, the tension in the string
A beam consisting of protons and electrons moving at the same speed goes through a thin region in which there is a magnetic field perpendicular to the beam. The protons and the electrons
A charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
A charged particle moves in a gravity-free space without change in velocity. Which of the following is/are possible?
(a) E = 0, B = 0
(b) E = 0, B ≠ 0
(c) E ≠ 0, B = 0
(d) E ≠ 0, B ≠ 0
If a charged particle moves unaccelerated in a region containing electric and magnetic fields
(a) `vecE "must be perpendicular" to vecB`
(b) `vecv "must be perpendicular" to vecE`
(c) must be perpendicular to v_B
Using the formula \[\vec{F} = q \vec{v} \times \vec{B} \text{ and } B = \frac{\mu_0 i}{2\pi r}\]show that the SI units of the magnetic field B and the permeability constant µ0 may be written as N mA−1 and NA−2 respectively.
A semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
A proton describes a circle of radius 1 cm in a magnetic field of strength 0.10 T. What would be the radius of the circle described by an α-particle moving with the same speed in the same magnetic field?
A circular coil of radius 2.0 cm has 500 turns and carries a current of 1.0 A. Its axis makes an angle of 30° with the uniform magnetic field of magnitude 0.40 T that exists in the space. Find the torque acting on the coil.
A particle of mass m and charge q is projected into a region that has a perpendicular magnetic field B. Find the angle of deviation (figure) of the particle as it comes out of the magnetic field if the width d of the region is very slightly smaller than
(a) `(mv)/(qB)` (b)`(mv)/(2qB)` (c)`(2mv)/(qB)`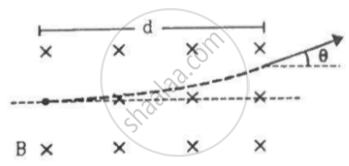
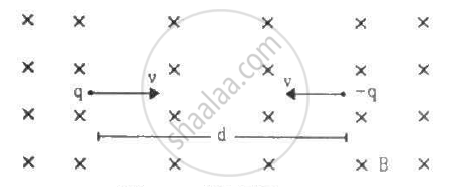
Two particles, each with mass m are placed at a separation d in a uniform magnetic field B, as shown in the figure. They have opposite charges of equal magnitude q. At time t = 0, the particles are projected towards each other, each with a speed v. Suppose the Coulomb force between the charges is switched off. (a) Find the maximum value vmof the projection speed, so that the two particles do not collide. (b) What would be the minimum and maximum separation between the particles if v = vm/2? (c) At what instant will a collision occur between the particles if v = 2vm? (d) Suppose v = 2vm and the collision between the particles is completely inelastic. Describe the motion after the collision.
A proton projected in a magnetic field of 0.020 T travels along a helical path of radius 5.0 cm and pitch 20 cm. Find the components of the velocity of the proton along and perpendicular to the magnetic field. Take the mass of the proton = 1.6 × 10−27 kg
A particle of mass m and charge q is released from the origin in a region in which the electric field and magnetic field are given by
`vecB = -B_0 vecj and vecE = E_0 vecK `
Find the speed of the particle as a function of its z-coordinate.
