Advertisements
Advertisements
प्रश्न
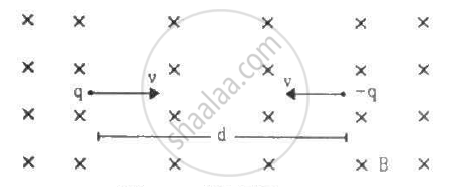
Two particles, each with mass m are placed at a separation d in a uniform magnetic field B, as shown in the figure. They have opposite charges of equal magnitude q. At time t = 0, the particles are projected towards each other, each with a speed v. Suppose the Coulomb force between the charges is switched off. (a) Find the maximum value vmof the projection speed, so that the two particles do not collide. (b) What would be the minimum and maximum separation between the particles if v = vm/2? (c) At what instant will a collision occur between the particles if v = 2vm? (d) Suppose v = 2vm and the collision between the particles is completely inelastic. Describe the motion after the collision.
उत्तर
Given,
Mass of two particles = m
Distance between them = d
Both the particles have equal charges in magnitude but opposite polarity equal to q.
As per the question, both the particles are projected towards each other with equal speed v.
It is assumed that Coulomb force between the charges is switched off.
(a) The maximum value vm of the projection speed so that the two particles do not collide:-
Both the particles will not collide if
d = r1 + r2 (where, r1 = r2 = radius of circular orbit described by the charged particles)
`⇒ d = (mv_m)/(qB) + (mv_m)/(qB) = (2mv_m)/(qB)`
`so, v_m = (qBd)/(2m)`
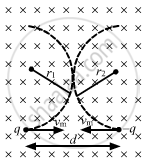
(b) The minimum and maximum separation between the particles if v = vm/2:-
Let the radius of the curved path taken by the particles, when they are projected with speed vm/2, be r.
So, minimum separation between the particles = (d - 2r)
`⇒ (d - 2r) = (2mv_m)/(qB) - (2mv)/(qB)`
`⇒ (d - 2r) = (mv_m)/(qB)`
`⇒ (d - 2r) = d/2`
Maximum distance separation = (d + 2r)
`⇒ d + 2r = d + d/2 = (3d)/2`
(c) The instant at which the collision occurs between the particles when
The particles will collide at a distance d/2 along the horizontal direction.
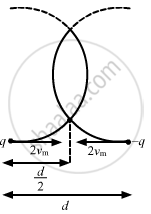
Let they collide after time t.
Velocity of the particles along the horizontal direction will remain the same.
Therefore, `t = d//2/(2v_m)`
`⇒ t = d/4xx(2m)/(qBd)`
(d) The motion of the two particles after collision when the collision is completely inelastic:-
v = 2vm
Let the particles collide at point P.
And at point P, both the particles will have motion in upward direction.
As the collision is inelastic they stick together.
Distance between centres = d
Velocity along the horizontal direction does not get affected due to the magnetic force.
At point P, velocities along the horizontal direction are equal and opposite. So, they cancel each other.
Velocity along the vertical direction (upward) will add up.
Magnetic force acting along the vertical direction,
`F=q(2v_m)B`
Acceleration along the vertical direction,
`a = F/m = (2qv_mB)/m`
Velocity of the combined mass at point P is along the vertical direction. So,
`v'= 0 + a × t`
`v' = 0 + ((2qv_mB)/(m))xx((m)/(2qb))`
`v' = v_m`
Hence, both the particles will behave as a combined mass and move with velocity vm.
APPEARS IN
संबंधित प्रश्न
Write the expression for the force `vecF` acting on a particle of mass m and charge q moving with velocity `vecV` in a magnetic field `vecB` , Under what conditions will it move in (i) a circular path and (ii) a helical path?
A proton and a deuteron having equal momenta enter in a region of a uniform magnetic field at right angle to the direction of a the field. Depict their trajectories in the field.
A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one point. If a magnetic field is switched on in the vertical direction, the tension in the string
If a charged particle at rest experiences no electromagnetic force,
(a) the electric field must be zero
(b) the magnetic field must be zero
(c) the electric field may or may not be zero
(d) the magnetic field may or may not be zero
If a charged particle projected in a gravity-free room deflects,
(a) there must be an electric field
(b) there must be a magnetic field
(c) both fields cannot be zero
(d) both fields can be non-zero
Consider three quantities \[x = E/B, y = \sqrt{1/ \mu_0 \epsilon_0}\] and \[z = \frac{l}{CR}\] . Here, l is the length of a wire, C is a capacitance and R is a resistance. All other symbols have standard meanings.
(a) x, y have the same dimensions.
(b) y, z have the same dimensions.
(c) z, x have the same dimensions.
(d) None of the three pairs have the same dimensions.
A current of 2 A enters at the corner d of a square frame abcd of side 20 cm and leaves at the opposite corner b. A magnetic field B = 0.1 T exists in the space in a direction perpendicular to the plane of the frame, as shown in the figure. Find the magnitude and direction of the magnetic forces on the four sides of the frame.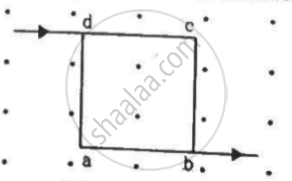
A semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
A wire, carrying a current i, is kept in the x−y plane along the curve y = A sin `((2x)/lamda x)`. magnetic field B exists in the z direction. Find the magnitude of the magnetic force on the portion of the wire between x = 0 and x = λ.
A particle of charge 2.0 × 10−8 C and mass 2.0 × 10−10 g is projected with a speed of 2.0 × 103 m s−1 in a region with a uniform magnetic field of 0.10 T. The velocity is perpendicular to the field. Find the radius of the circle formed by the particle and also the time period.
An electron of kinetic energy 100 eV circulates in a path of radius 10 cm in a magnetic field. Find the magnetic field and the number of revolutions per second made by the electron.
A circular coil of radius 2.0 cm has 500 turns and carries a current of 1.0 A. Its axis makes an angle of 30° with the uniform magnetic field of magnitude 0.40 T that exists in the space. Find the torque acting on the coil.
A square coil of edge l and with n turns carries a current i. It is kept on a smooth horizontal plate. A uniform magnetic field B exists parallel to an edge. The total mass of the coil is M. What should be the minimum value of B for which the coil will start tipping over?
A charged particle is accelerated through a potential difference of 12 kV and acquires a speed of 1.0 × 106 m s−1. It is then injected perpendicularly into a magnetic field of strength 0.2 T. Find the radius of the circle described by it.
A narrow beam of singly-charged carbon ions, moving at a constant velocity of 6.0 × 104m s−1, is sent perpendicularly in a rectangular region of uniform magnetic field B = 0.5 T (figure). It is found that two beams emerge from the field in the backward direction, the separations from the incident beam being 3.0 cm and 3.5 cm. Identify the isotopes present in the ion beam. Take the mass of an ion = A(1.6 × 10−27) kg, where A is the mass number.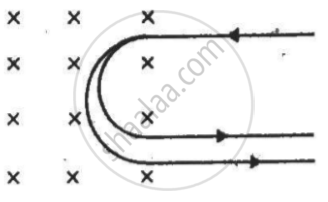
A narrow beam of singly charged potassium ions of kinetic energy 32 keV is injected into a region of width 1.00 cm with a magnetic field of strength 0.500 T, as shown in the figure. The ions are collected at a screen 95.5 cm away from the field region. If the beam contains isotopes of atomic weights 39 and 41, find the separation between the points where these isotopes strike the screen. Take the mass of a potassium ion = A (1.6 × 10−27) kg, where A is the mass number.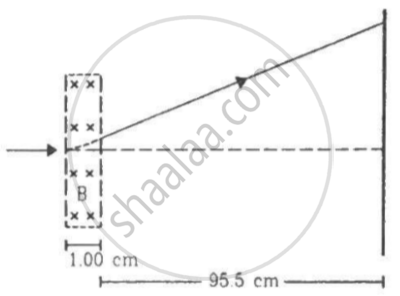
The figure shows a convex lens of focal length 12 cm lying in a uniform magnetic field Bof magnitude 1.2 T parallel to its principal axis. A particle with charge 2.0 × 10−3 C and mass 2.0 × 10−5 kg is projected perpendicular to the plane of the diagram with a speed of 4.8 m s−1. The particle moves along a circle with its centre on the principal axis at a distance of 18 cm from the lens. Show that the image of the particle moves along a circle and find the radius of that circle.

A uniform magnetic field of magnitude 0.20 T exists in space from east to west. With what speed should a particle of mass 0.010 g and with charge 1.0 × 10−5 C be projected from south to north so that it moves with uniform velocity?
The velocity of a body of mass 2 kg as a function of time t is given by v(t) = 2t`hat"i" + "t"^2hat"j"`. The force acting on it, at time t = 2 s is given by ______.
