Advertisements
Advertisements
प्रश्न
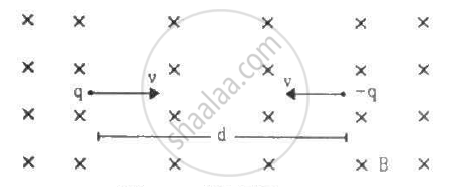
Two particles, each with mass m are placed at a separation d in a uniform magnetic field B, as shown in the figure. They have opposite charges of equal magnitude q. At time t = 0, the particles are projected towards each other, each with a speed v. Suppose the Coulomb force between the charges is switched off. (a) Find the maximum value vmof the projection speed, so that the two particles do not collide. (b) What would be the minimum and maximum separation between the particles if v = vm/2? (c) At what instant will a collision occur between the particles if v = 2vm? (d) Suppose v = 2vm and the collision between the particles is completely inelastic. Describe the motion after the collision.
उत्तर
Given,
Mass of two particles = m
Distance between them = d
Both the particles have equal charges in magnitude but opposite polarity equal to q.
As per the question, both the particles are projected towards each other with equal speed v.
It is assumed that Coulomb force between the charges is switched off.
(a) The maximum value vm of the projection speed so that the two particles do not collide:-
Both the particles will not collide if
d = r1 + r2 (where, r1 = r2 = radius of circular orbit described by the charged particles)
`⇒ d = (mv_m)/(qB) + (mv_m)/(qB) = (2mv_m)/(qB)`
`so, v_m = (qBd)/(2m)`
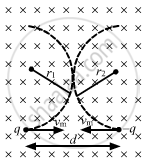
(b) The minimum and maximum separation between the particles if v = vm/2:-
Let the radius of the curved path taken by the particles, when they are projected with speed vm/2, be r.
So, minimum separation between the particles = (d - 2r)
`⇒ (d - 2r) = (2mv_m)/(qB) - (2mv)/(qB)`
`⇒ (d - 2r) = (mv_m)/(qB)`
`⇒ (d - 2r) = d/2`
Maximum distance separation = (d + 2r)
`⇒ d + 2r = d + d/2 = (3d)/2`
(c) The instant at which the collision occurs between the particles when
The particles will collide at a distance d/2 along the horizontal direction.
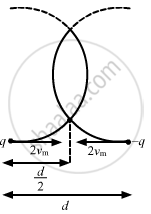
Let they collide after time t.
Velocity of the particles along the horizontal direction will remain the same.
Therefore, `t = d//2/(2v_m)`
`⇒ t = d/4xx(2m)/(qBd)`
(d) The motion of the two particles after collision when the collision is completely inelastic:-
v = 2vm
Let the particles collide at point P.
And at point P, both the particles will have motion in upward direction.
As the collision is inelastic they stick together.
Distance between centres = d
Velocity along the horizontal direction does not get affected due to the magnetic force.
At point P, velocities along the horizontal direction are equal and opposite. So, they cancel each other.
Velocity along the vertical direction (upward) will add up.
Magnetic force acting along the vertical direction,
`F=q(2v_m)B`
Acceleration along the vertical direction,
`a = F/m = (2qv_mB)/m`
Velocity of the combined mass at point P is along the vertical direction. So,
`v'= 0 + a × t`
`v' = 0 + ((2qv_mB)/(m))xx((m)/(2qb))`
`v' = v_m`
Hence, both the particles will behave as a combined mass and move with velocity vm.
APPEARS IN
संबंधित प्रश्न
Write the expression for the force `vecF` acting on a particle of mass m and charge q moving with velocity `vecV` in a magnetic field `vecB` , Under what conditions will it move in (i) a circular path and (ii) a helical path?
A proton and an α-particle move perpendicular to a magnetic field. Find the ratio of radii of circular paths described by them when both have (i) equal velocities, and (ii) equal kinetic energy.
A straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid air by a uniform magnetic field B. What is the magnitude of the magnetic field?
Write the expression for the force,`vecF` acting on a charged particle of charge ‘q’, moving with a velocity `vecV` in the presence of both electric field `vecF`and magnetic field `vecB` . Obtain the condition under which the particle moves undeflected through the fields.
Assume that the magnetic field is uniform in a cubical region and zero outside. Can you project a charged particle from outside into the field, so that the particle describes a complete circle in the field?
A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one point. If a magnetic field is switched on in the vertical direction, the tension in the string
A charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
A charged particle moves along a circle under the action of possible constant electric and magnetic fields. Which of the following is possible?
(a) E = 0, B = 0
(b) E = 0, B ≠ 0
(c) E ≠ 0, B = 0
(d) E ≠ 0, B ≠ 0
When a proton is released from rest in a room, it starts with an initial acceleration a0towards west. When it is projected towards north with a speed v0, it moves with an initial acceleration 3a0 towards west. Find the electric field and the maximum possible magnetic field in the room.
A semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
A charged particle is accelerated through a potential difference of 12 kV and acquires a speed of 1.0 × 106 m s−1. It is then injected perpendicularly into a magnetic field of strength 0.2 T. Find the radius of the circle described by it.
The figure shows a convex lens of focal length 12 cm lying in a uniform magnetic field Bof magnitude 1.2 T parallel to its principal axis. A particle with charge 2.0 × 10−3 C and mass 2.0 × 10−5 kg is projected perpendicular to the plane of the diagram with a speed of 4.8 m s−1. The particle moves along a circle with its centre on the principal axis at a distance of 18 cm from the lens. Show that the image of the particle moves along a circle and find the radius of that circle.

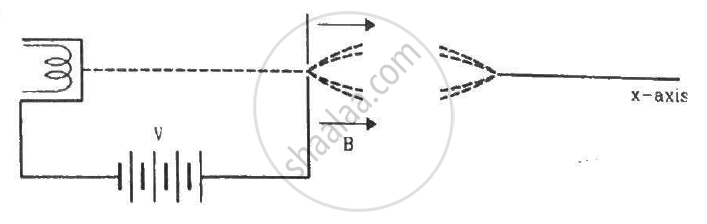
Electrons emitted with negligible speed from an electron gun are accelerated through a potential difference V along the x-axis. These electrons emerge from a narrow hole into a uniform magnetic field B directed along this axis. However, some of the electrons emerging from the hole make slightly divergent angles, as shown in the figure. Show that these paraxial electrons are refocussed on the x-axis at a distance `sqrt(8pi^2mV)/(eB^2).`
A uniform magnetic field of magnitude 0.20 T exists in space from east to west. With what speed should a particle of mass 0.010 g and with charge 1.0 × 10−5 C be projected from south to north so that it moves with uniform velocity?
A particle with a charge of 5.0 µC and a mass of 5.0 × 10−12 kg is projected with a speed of 1.0 km s−1 in a magnetic field of magnitude 5.0 mT. The angle between the magnetic field and the velocity is sin−1 (0.90). Show that the path of the particle will be a helix. Find the diameter of the helix and its pitch.
A proton projected in a magnetic field of 0.020 T travels along a helical path of radius 5.0 cm and pitch 20 cm. Find the components of the velocity of the proton along and perpendicular to the magnetic field. Take the mass of the proton = 1.6 × 10−27 kg
A particle of mass m and charge q is released from the origin in a region in which the electric field and magnetic field are given by
`vecB = -B_0 vecj and vecE = E_0 vecK `
Find the speed of the particle as a function of its z-coordinate.
The velocity of a body of mass 2 kg as a function of time t is given by v(t) = 2t`hat"i" + "t"^2hat"j"`. The force acting on it, at time t = 2 s is given by ______.
