Advertisements
Advertisements
प्रश्न
A semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
उत्तर
Given,
Radius of semicircular wire, r = 5.0 cm
Thus, the length of the wire = 2r
Electric current flowing through wire = 5.0 A
Magnetic field, B = 0.50 T
Direction of magnetic field is perpendicular to the plane of the wire which implies that angle between length of the wire and magnetic field, θ = 90˚
As we know the magnetic force is given by
`vecF = I vecl xx vecB`
`vecF = I2rBsin90^circ`
= 5 × 2 × 0.5 × =0.25 N
APPEARS IN
संबंधित प्रश्न
A moving charged particle q travelling along the positive x-axis enters a uniform magnetic field B.
When will the force acting on q be maximum?
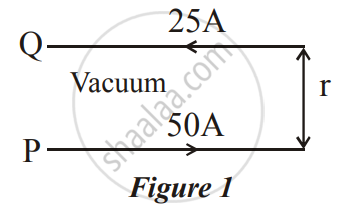
A long horizontal wire P carries a current of 50A. It is rigidly fixed. Another wire Q is placed directly above and parallel to P, as shown in Figure 1 below. The weight per unit length of the wire Q is 0.025 Nm-1 and it carries a current of 25A. Find the distance 'r' of the wire Q from the wire P so that the wire Q remains at rest
A proton and a deuteron having equal momenta enter in a region of a uniform magnetic field at right angle to the direction of a the field. Depict their trajectories in the field.
Assume that the magnetic field is uniform in a cubical region and zero outside. Can you project a charged particle from outside into the field, so that the particle describes a complete circle in the field?
A beam consisting of protons and electrons moving at the same speed goes through a thin region in which there is a magnetic field perpendicular to the beam. The protons and the electrons
A charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
A magnetic field of \[(4.0\times10^-3 \overrightarrow k)\] T exerts a force of \[(4.0 \overrightarrow i + 3.0 \overrightarrow j ) \times 10^{−10} N\] on a particle with a charge of 1.0 × 10−9 C and going in the x − y plane. Find the velocity of the particle.
When a proton is released from rest in a room, it starts with an initial acceleration a0towards west. When it is projected towards north with a speed v0, it moves with an initial acceleration 3a0 towards west. Find the electric field and the maximum possible magnetic field in the room.
A magnetic field of strength 1.0 T is produced by a strong electromagnet in a cylindrical region of radius 4.0 cm, as shown in the figure. A wire, carrying a current of 2.0 A, is placed perpendicular to and intersecting the axis of the cylindrical region. Find the magnitude of the force acting on the wire.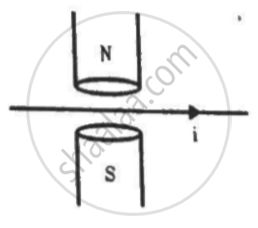
A wire, carrying a current i, is kept in the x−y plane along the curve y = A sin `((2x)/lamda x)`. magnetic field B exists in the z direction. Find the magnitude of the magnetic force on the portion of the wire between x = 0 and x = λ.
Consider a non-conducting ring of radius r and mass m that has a total charge qdistributed uniformly on it. The ring is rotated about its axis with an angular speed ω. (a) Find the equivalent electric current in the ring. (b) Find the magnetic moment µ of the ring. (c) Show that `pi = (q)/(2m)` l, where l is the angular momentum of the ring about its axis of rotation.
A narrow beam of singly charged potassium ions of kinetic energy 32 keV is injected into a region of width 1.00 cm with a magnetic field of strength 0.500 T, as shown in the figure. The ions are collected at a screen 95.5 cm away from the field region. If the beam contains isotopes of atomic weights 39 and 41, find the separation between the points where these isotopes strike the screen. Take the mass of a potassium ion = A (1.6 × 10−27) kg, where A is the mass number.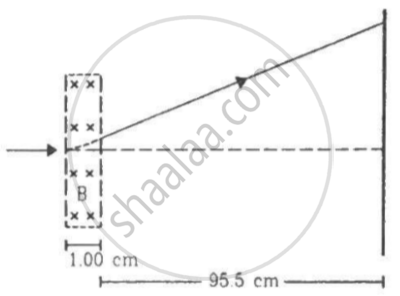
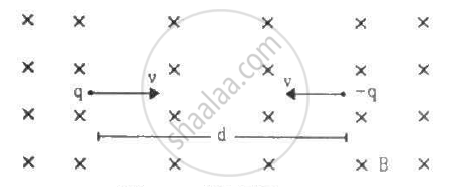
Two particles, each with mass m are placed at a separation d in a uniform magnetic field B, as shown in the figure. They have opposite charges of equal magnitude q. At time t = 0, the particles are projected towards each other, each with a speed v. Suppose the Coulomb force between the charges is switched off. (a) Find the maximum value vmof the projection speed, so that the two particles do not collide. (b) What would be the minimum and maximum separation between the particles if v = vm/2? (c) At what instant will a collision occur between the particles if v = 2vm? (d) Suppose v = 2vm and the collision between the particles is completely inelastic. Describe the motion after the collision.
A particle moves in a circle of diameter 1.0 cm under the action of a magnetic field of 0.40 T. An electric field of 200 V m−1 makes the path straight. Find the charge/mass ratio of the particle.
A uniform magnetic field of 1.5 T exists in a cylindrical region of radius 10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if,
(a) the wire intersects the axis,
(b) the wire is turned from N-S to northeast-northwest direction,
(c) the wire in the N-S direction is lowered from the axis by a distance of 6.0 cm?
Current flows through uniform, square frames as shown in the figure. In which case is the magnetic field at the centre of the frame not zero?
