Advertisements
Advertisements
प्रश्न
A narrow beam of singly charged potassium ions of kinetic energy 32 keV is injected into a region of width 1.00 cm with a magnetic field of strength 0.500 T, as shown in the figure. The ions are collected at a screen 95.5 cm away from the field region. If the beam contains isotopes of atomic weights 39 and 41, find the separation between the points where these isotopes strike the screen. Take the mass of a potassium ion = A (1.6 × 10−27) kg, where A is the mass number.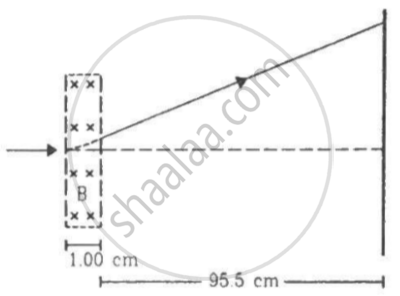
उत्तर
Kinetic energy of singly-charged potassium ions = 32 keV
Width of the magnetic region = 1.00 cm
Magnetic field's strength, B = 0.500 T
Distance between the screen and the region = 95.5 cm
Atomic weights of the two isotopes are 39 and 41.
Mass of a potassium ion = A (1.6 × 10−27) kg
For a singly-charged potassium ion K-39 :
Mass of K-39 = 39 × 1.6 × 10−27 kg,
Charge, q = 1.6 × 10−19 C
As per the question, the narrow beam of singly-charged potassium ions is injected into a region of magnetic field.
As
K.E = 32 keV
`1/2 mv^2 = 32 xx 10^3 xx 1.6 xx 10^-19`
`1/2`× 39 × (1.6 × 10−27) × v2 = 32 × 103 × 1.6 × 10−19
v = 4.05 × 105
We know that throughout the motion, the horizontal velocity remains constant.
So, the time taken to cross the magnetic field,
t = `d/v = (0.01)/(4.05xx10^5)`
= 24.7 × 10−9 s
Now, the acceleration in the magnetic field region:
F = qvB = ma
`a = (qvB)/(m)`
= `(1.6xx10^-19xx4.05xx10^5)/(39xx1.6xx10^-27)`
= 5192 × 108 m/s2
Velocity in the vertical direction, vy = at
= 5193.53 × 108 × 24.7 × 10−9
= 12824.24 m/s
Time taken to reach the screen
`d/v = (0.955)/(4.05xx10^5)`
Distance moved vertically in this time
= vy × t
= 12824.24 × 2358 × 10−9
= 3023.95×10-5 m
Vertical distance travelled by the particle inside magnetic field can be found out by using equaton of motion
v2 = 2aS
⇒ (12824.24)2 = 2 × 5192 × 108 × S
⇒ 15.83×10−5 = S
Net display from line
= 15.83×10−5+3023.95×10-5
= 3039.787×10−5 m.
For the potassium ion K-41l :
`1/2`× 41 × 1.6 × 10−27 v2= 32 × 103 × 1.6 × 10−9
⇒ v = 3.94×105 m/s
Similarly, acceleration,
a = 4805 × 108 m/s2
t = time taken for exiting the magnetic field
= 25.4 × 10−9 sec.
vy1= at (vertical velocity)
= 4805 × 108 × 25.4 × 10−9
= 12204.7× 10−9 m/s
Time to reach the screen
= 2423× 10−9 s.
Distance moved vertically
= 12204.7 × 2423 × 10−9
= 2957.1× 10−5
Now,
Vertical distance travelled by the particle inside magnetic field can be found out by using equaton of motion
v2 = 2aS
(12204.7)2 = 2 × 4805 × 108 S
⇒ S = 15.49× 10-5 m
Net distance travelled
= 15.49× 10-5 +2957.1× 10−5
= 2972.68× 10-5 m.
Net gap between K-39 and K-41
= 3039.787×10−5− 2972.68× 10-5
= 67 mm.
APPEARS IN
संबंधित प्रश्न
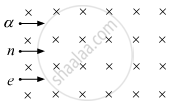
A neutron, an electron and an alpha particle, moving with equal velocities, enter a uniform magnetic field going into the plane of the paper, as shown. Trace their paths in the field and justify your answer.
If a charged particle projected in a gravity-free room deflects,
(a) there must be an electric field
(b) there must be a magnetic field
(c) both fields cannot be zero
(d) both fields can be non-zero
A charged particle moves in a gravity-free space without change in velocity. Which of the following is/are possible?
(a) E = 0, B = 0
(b) E = 0, B ≠ 0
(c) E ≠ 0, B = 0
(d) E ≠ 0, B ≠ 0
If a charged particle moves unaccelerated in a region containing electric and magnetic fields
(a) `vecE "must be perpendicular" to vecB`
(b) `vecv "must be perpendicular" to vecE`
(c) must be perpendicular to v_B
A magnetic field of \[(4.0\times10^-3 \overrightarrow k)\] T exerts a force of \[(4.0 \overrightarrow i + 3.0 \overrightarrow j ) \times 10^{−10} N\] on a particle with a charge of 1.0 × 10−9 C and going in the x − y plane. Find the velocity of the particle.
Consider three quantities \[x = E/B, y = \sqrt{1/ \mu_0 \epsilon_0}\] and \[z = \frac{l}{CR}\] . Here, l is the length of a wire, C is a capacitance and R is a resistance. All other symbols have standard meanings.
(a) x, y have the same dimensions.
(b) y, z have the same dimensions.
(c) z, x have the same dimensions.
(d) None of the three pairs have the same dimensions.
A current of 2 A enters at the corner d of a square frame abcd of side 20 cm and leaves at the opposite corner b. A magnetic field B = 0.1 T exists in the space in a direction perpendicular to the plane of the frame, as shown in the figure. Find the magnitude and direction of the magnetic forces on the four sides of the frame.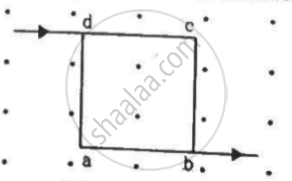
A semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
An electron of kinetic energy 100 eV circulates in a path of radius 10 cm in a magnetic field. Find the magnetic field and the number of revolutions per second made by the electron.
Consider a non-conducting ring of radius r and mass m that has a total charge qdistributed uniformly on it. The ring is rotated about its axis with an angular speed ω. (a) Find the equivalent electric current in the ring. (b) Find the magnetic moment µ of the ring. (c) Show that `pi = (q)/(2m)` l, where l is the angular momentum of the ring about its axis of rotation.
A particle of mass m and charge q is projected into a region that has a perpendicular magnetic field B. Find the angle of deviation (figure) of the particle as it comes out of the magnetic field if the width d of the region is very slightly smaller than
(a) `(mv)/(qB)` (b)`(mv)/(2qB)` (c)`(2mv)/(qB)`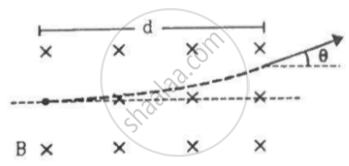
A narrow beam of singly-charged carbon ions, moving at a constant velocity of 6.0 × 104m s−1, is sent perpendicularly in a rectangular region of uniform magnetic field B = 0.5 T (figure). It is found that two beams emerge from the field in the backward direction, the separations from the incident beam being 3.0 cm and 3.5 cm. Identify the isotopes present in the ion beam. Take the mass of an ion = A(1.6 × 10−27) kg, where A is the mass number.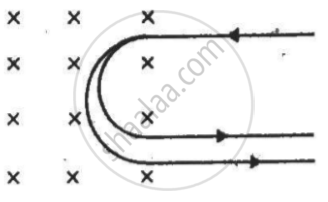
A uniform magnetic field of magnitude 0.20 T exists in space from east to west. With what speed should a particle of mass 0.010 g and with charge 1.0 × 10−5 C be projected from south to north so that it moves with uniform velocity?
A particle moves in a circle of diameter 1.0 cm under the action of a magnetic field of 0.40 T. An electric field of 200 V m−1 makes the path straight. Find the charge/mass ratio of the particle.
A uniform magnetic field of 1.5 T exists in a cylindrical region of radius 10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if,
(a) the wire intersects the axis,
(b) the wire is turned from N-S to northeast-northwest direction,
(c) the wire in the N-S direction is lowered from the axis by a distance of 6.0 cm?
The velocity of a body of mass 2 kg as a function of time t is given by v(t) = 2t`hat"i" + "t"^2hat"j"`. The force acting on it, at time t = 2 s is given by ______.
A particle of mass 10 mg and having a charge of 50 mC is projected with a speed of 15 m/s into a uniform magnetic field of 125 mT. Assuming that the particle is projected with its velocity perpendicular to the magnetic field, the time after which the particle reaches its original position for the first time is ______.
