Advertisements
Advertisements
प्रश्न
If a charged particle projected in a gravity-free room deflects,
(a) there must be an electric field
(b) there must be a magnetic field
(c) both fields cannot be zero
(d) both fields can be non-zero
उत्तर
(c) both fields cannot be zero
(d) both fields can be nonzero
As the particle gets deflected, a force acts on the particle. So, either it has got deflected due to the magnetic force or electric force; so, both the fields cannot be zero. Also, the particle can be deflected under the combined effect of magnetic and electric forces; so, both fields can be non-zero.
APPEARS IN
संबंधित प्रश्न
Show that the kinetic energy of the particle moving in a magnetic field remains constant.
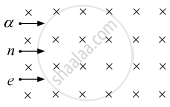
A neutron, an electron and an alpha particle, moving with equal velocities, enter a uniform magnetic field going into the plane of the paper, as shown. Trace their paths in the field and justify your answer.
A proton and an α-particle move perpendicular to a magnetic field. Find the ratio of radii of circular paths described by them when both have (i) equal velocities, and (ii) equal kinetic energy.
A straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid air by a uniform magnetic field B. What is the magnitude of the magnetic field?
Two particles X and Y having equal charge, after being accelerated through the same potential difference enter a region of uniform magnetic field and describe circular paths of radii R1 and R2 respectively. The ratio of the mass of X to that of Y is ______.
When a proton is released from rest in a room, it starts with an initial acceleration a0towards west. When it is projected towards north with a speed v0, it moves with an initial acceleration 3a0 towards west. Find the electric field and the maximum possible magnetic field in the room.
A current of 2 A enters at the corner d of a square frame abcd of side 20 cm and leaves at the opposite corner b. A magnetic field B = 0.1 T exists in the space in a direction perpendicular to the plane of the frame, as shown in the figure. Find the magnitude and direction of the magnetic forces on the four sides of the frame.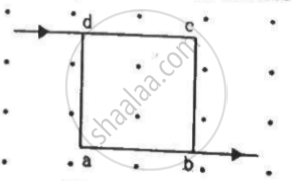
Using the formula \[\vec{F} = q \vec{v} \times \vec{B} \text{ and } B = \frac{\mu_0 i}{2\pi r}\]show that the SI units of the magnetic field B and the permeability constant µ0 may be written as N mA−1 and NA−2 respectively.
A particle of charge 2.0 × 10−8 C and mass 2.0 × 10−10 g is projected with a speed of 2.0 × 103 m s−1 in a region with a uniform magnetic field of 0.10 T. The velocity is perpendicular to the field. Find the radius of the circle formed by the particle and also the time period.
Protons with kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field, so that it just misses a plane target kept at a distance l in front of the accelerator. Find the magnetic field.
A square coil of edge l and with n turns carries a current i. It is kept on a smooth horizontal plate. A uniform magnetic field B exists parallel to an edge. The total mass of the coil is M. What should be the minimum value of B for which the coil will start tipping over?
A narrow beam of singly charged potassium ions of kinetic energy 32 keV is injected into a region of width 1.00 cm with a magnetic field of strength 0.500 T, as shown in the figure. The ions are collected at a screen 95.5 cm away from the field region. If the beam contains isotopes of atomic weights 39 and 41, find the separation between the points where these isotopes strike the screen. Take the mass of a potassium ion = A (1.6 × 10−27) kg, where A is the mass number.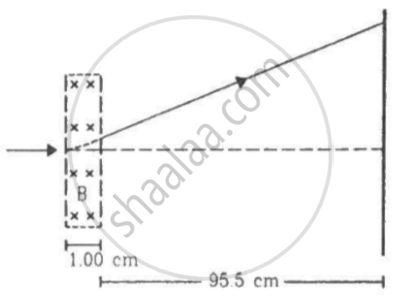
Doubly-ionised helium ions are projected with a speed of 10 km s−1 in a direction perpendicular to a uniform magnetic field of magnitude 1.0 T. Find (a) the force acting on an ion (b) the radius of the circle in which it circulates and (c) the time taken by an ion to complete the circle.
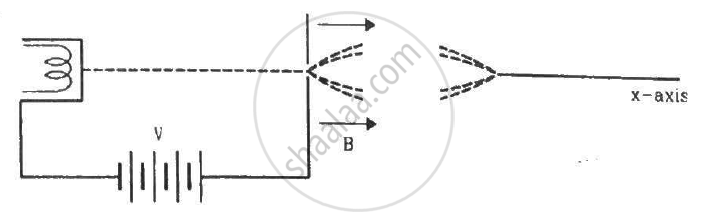
Electrons emitted with negligible speed from an electron gun are accelerated through a potential difference V along the x-axis. These electrons emerge from a narrow hole into a uniform magnetic field B directed along this axis. However, some of the electrons emerging from the hole make slightly divergent angles, as shown in the figure. Show that these paraxial electrons are refocussed on the x-axis at a distance `sqrt(8pi^2mV)/(eB^2).`
A long, straight wire carrying a current of 30 A is placed in an external, uniform magnetic field of 4.0 × 10−4 T parallel to the current. Find the magnitude of the resultant magnetic field at a point 2.0 cm away from the wire.
Current flows through uniform, square frames as shown in the figure. In which case is the magnetic field at the centre of the frame not zero?
A particle of mass 10 mg and having a charge of 50 mC is projected with a speed of 15 m/s into a uniform magnetic field of 125 mT. Assuming that the particle is projected with its velocity perpendicular to the magnetic field, the time after which the particle reaches its original position for the first time is ______.
