Advertisements
Advertisements
प्रश्न
A magnetic field of \[(4.0\times10^-3 \overrightarrow k)\] T exerts a force of \[(4.0 \overrightarrow i + 3.0 \overrightarrow j ) \times 10^{−10} N\] on a particle with a charge of 1.0 × 10−9 C and going in the x − y plane. Find the velocity of the particle.
उत्तर
Given:-
Magnetic field, B = `(4xx10xx^-3 hatK)`T
Force exerted by the magnetic field on the charged particle, F = `(4 hati + 3hatj )`× 10−10 N
Charge of the particle, q = 1 × 10−9 C
As per the question, the charge is going in the X-Y plane.
So, the x-component of force, Fx = 4 × 10−10 N
and the y-component of force, Fy = 3 × 10−10 N
Considering the motion along x-axis:-
Fx = qvy×B
On putting the respective values, we get:-
vy = 100 m/s
Motion along y-axis:-
Fy = qvx×B
⇒ vx = 75 m/s
Thus, total velocity =`( -75 vec i + 100 vec j) `m/s
APPEARS IN
संबंधित प्रश्न
Show that the kinetic energy of the particle moving in a magnetic field remains constant.
A neutron, an electron and an alpha particle, moving with equal velocities, enter a uniform magnetic field going into the plane of the paper, as shown. Trace their paths in the field and justify your answer.
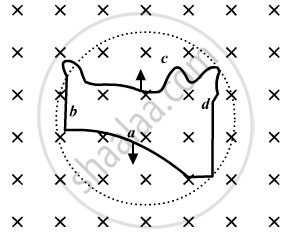
A flexible wire of irregular shape, abcd, as shown in the figure, turns into a circular shape when placed in a region of magnetic field which is directed normal to the plane of the loop away from the reader. Predict the direction of the induced current in the wire.
A proton and a deuteron having equal momenta enter in a region of a uniform magnetic field at right angle to the direction of a the field. Depict their trajectories in the field.
A charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
A charged particle moves along a circle under the action of possible constant electric and magnetic fields. Which of the following is possible?
(a) E = 0, B = 0
(b) E = 0, B ≠ 0
(c) E ≠ 0, B = 0
(d) E ≠ 0, B ≠ 0
When a proton is released from rest in a room, it starts with an initial acceleration a0towards west. When it is projected towards north with a speed v0, it moves with an initial acceleration 3a0 towards west. Find the electric field and the maximum possible magnetic field in the room.
A magnetic field of strength 1.0 T is produced by a strong electromagnet in a cylindrical region of radius 4.0 cm, as shown in the figure. A wire, carrying a current of 2.0 A, is placed perpendicular to and intersecting the axis of the cylindrical region. Find the magnitude of the force acting on the wire.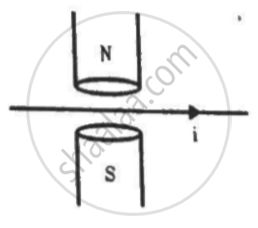
A semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
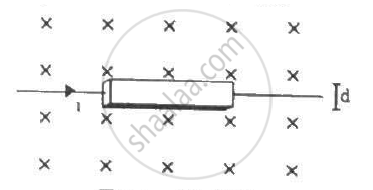
A current i is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n. (a) Find the drift velocity v of the electrons. (b) If a magnetic field B exists in the region, as shown in the figure, what is the average magnetic force on the free electrons? (c) Due to the magnetic force, the free electrons get accumulated on one side of the conductor along its length. This produces a transverse electric field in the conductor, which opposes the magnetic force on the electrons. Find the magnitude of the electric field which will stop further accumulation of electrons. (d) What will be the potential difference developed across the width of the conductor due to the electron-accumulation? The appearance of a transverse emf, when a current-carrying wire is placed in a magnetic field, is called Hall effect.
An electron of kinetic energy 100 eV circulates in a path of radius 10 cm in a magnetic field. Find the magnetic field and the number of revolutions per second made by the electron.
A circular coil of radius 2.0 cm has 500 turns and carries a current of 1.0 A. Its axis makes an angle of 30° with the uniform magnetic field of magnitude 0.40 T that exists in the space. Find the torque acting on the coil.
A charged particle is accelerated through a potential difference of 12 kV and acquires a speed of 1.0 × 106 m s−1. It is then injected perpendicularly into a magnetic field of strength 0.2 T. Find the radius of the circle described by it.
A proton is projected with a velocity of 3 × 106 m s−1 perpendicular to a uniform magnetic field of 0.6 T. Find the acceleration of the proton.
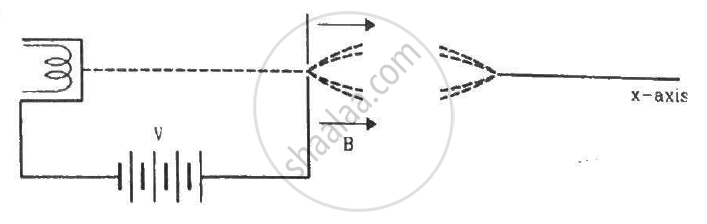
Electrons emitted with negligible speed from an electron gun are accelerated through a potential difference V along the x-axis. These electrons emerge from a narrow hole into a uniform magnetic field B directed along this axis. However, some of the electrons emerging from the hole make slightly divergent angles, as shown in the figure. Show that these paraxial electrons are refocussed on the x-axis at a distance `sqrt(8pi^2mV)/(eB^2).`
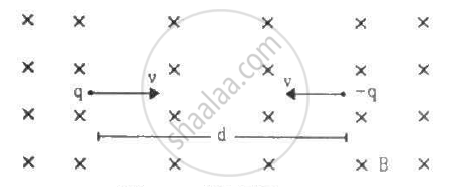
Two particles, each with mass m are placed at a separation d in a uniform magnetic field B, as shown in the figure. They have opposite charges of equal magnitude q. At time t = 0, the particles are projected towards each other, each with a speed v. Suppose the Coulomb force between the charges is switched off. (a) Find the maximum value vmof the projection speed, so that the two particles do not collide. (b) What would be the minimum and maximum separation between the particles if v = vm/2? (c) At what instant will a collision occur between the particles if v = 2vm? (d) Suppose v = 2vm and the collision between the particles is completely inelastic. Describe the motion after the collision.
A uniform magnetic field of magnitude 0.20 T exists in space from east to west. With what speed should a particle of mass 0.010 g and with charge 1.0 × 10−5 C be projected from south to north so that it moves with uniform velocity?
A particle with a charge of 5.0 µC and a mass of 5.0 × 10−12 kg is projected with a speed of 1.0 km s−1 in a magnetic field of magnitude 5.0 mT. The angle between the magnetic field and the velocity is sin−1 (0.90). Show that the path of the particle will be a helix. Find the diameter of the helix and its pitch.
A uniform magnetic field of 1.5 T exists in a cylindrical region of radius 10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if,
(a) the wire intersects the axis,
(b) the wire is turned from N-S to northeast-northwest direction,
(c) the wire in the N-S direction is lowered from the axis by a distance of 6.0 cm?
