Advertisements
Advertisements
प्रश्न
A beam consisting of protons and electrons moving at the same speed goes through a thin region in which there is a magnetic field perpendicular to the beam. The protons and the electrons
पर्याय
will go undeviated
will be deviated by the same angle and will not separate
will be deviated by different angles and hence will separate
will be deviated by the same angle but will separate
उत्तर
will be deviated by different angles and hence will separate
Force on a charged particle, F = qVB
For an electron, this force is F = -eVB, whereas on a proton this force is F = eVB.
Here, 'e' is the charge of the electron. So, from the above formulas, we can see that electrons and protons will experience equal force but in opposite directions; so they separate out. In other words, we can say that they are deviated by different angles and causes them to separate.
APPEARS IN
संबंधित प्रश्न
A moving charged particle q travelling along the positive x-axis enters a uniform magnetic field B.
When will the force acting on q be maximum?
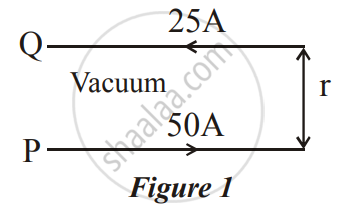
A long horizontal wire P carries a current of 50A. It is rigidly fixed. Another wire Q is placed directly above and parallel to P, as shown in Figure 1 below. The weight per unit length of the wire Q is 0.025 Nm-1 and it carries a current of 25A. Find the distance 'r' of the wire Q from the wire P so that the wire Q remains at rest
A proton and a deuteron having equal momenta enter in a region of a uniform magnetic field at right angle to the direction of a the field. Depict their trajectories in the field.
Assume that the magnetic field is uniform in a cubical region and zero outside. Can you project a charged particle from outside into the field, so that the particle describes a complete circle in the field?
A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one point. If a magnetic field is switched on in the vertical direction, the tension in the string
An electric current i enters and leaves a uniform circular wire of radius a through diametrically opposite points. A charged particle q, moving along the axis of the circular wire, passes through its centre at speed v. The magnetic force acting on the particle, when it passes through the centre, has a magnitude equal to
A charged particle moves in a gravity-free space without change in velocity. Which of the following is/are possible?
(a) E = 0, B = 0
(b) E = 0, B ≠ 0
(c) E ≠ 0, B = 0
(d) E ≠ 0, B ≠ 0
A particle is projected in a plane perpendicular to a uniform magnetic field. The area bounded by the path described by the particle is proportional to
Consider three quantities \[x = E/B, y = \sqrt{1/ \mu_0 \epsilon_0}\] and \[z = \frac{l}{CR}\] . Here, l is the length of a wire, C is a capacitance and R is a resistance. All other symbols have standard meanings.
(a) x, y have the same dimensions.
(b) y, z have the same dimensions.
(c) z, x have the same dimensions.
(d) None of the three pairs have the same dimensions.
A metal wire PQ of mass 10 g lies at rest on two horizontal metal rails separated by 4.90 cm (figure). A vertically-downward magnetic field of magnitude 0.800 T exists in the space. The resistance of the circuit is slowly decreased and it is found that when the resistance goes below 20.0 Ω, the wire PQ starts sliding on the rails. Find the coefficient of friction.
A proton describes a circle of radius 1 cm in a magnetic field of strength 0.10 T. What would be the radius of the circle described by an α-particle moving with the same speed in the same magnetic field?
Consider a non-conducting ring of radius r and mass m that has a total charge qdistributed uniformly on it. The ring is rotated about its axis with an angular speed ω. (a) Find the equivalent electric current in the ring. (b) Find the magnetic moment µ of the ring. (c) Show that `pi = (q)/(2m)` l, where l is the angular momentum of the ring about its axis of rotation.
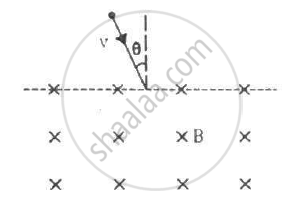
A particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B, as shown in the figure. (a) Find the radius of the circular arc it describes in the magnetic field. (b) Find the angle subtended by the arc at the centre. (c) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.
A particle of mass m and charge q is projected into a region that has a perpendicular magnetic field B. Find the angle of deviation (figure) of the particle as it comes out of the magnetic field if the width d of the region is very slightly smaller than
(a) `(mv)/(qB)` (b)`(mv)/(2qB)` (c)`(2mv)/(qB)`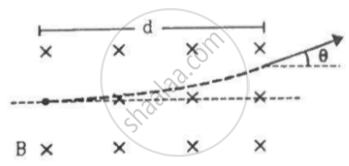
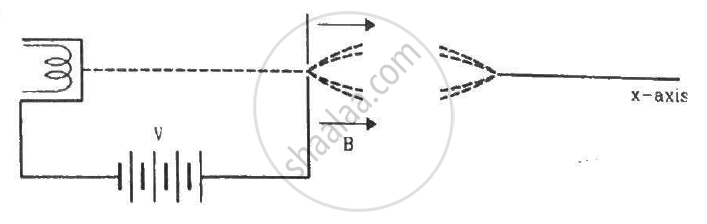
Electrons emitted with negligible speed from an electron gun are accelerated through a potential difference V along the x-axis. These electrons emerge from a narrow hole into a uniform magnetic field B directed along this axis. However, some of the electrons emerging from the hole make slightly divergent angles, as shown in the figure. Show that these paraxial electrons are refocussed on the x-axis at a distance `sqrt(8pi^2mV)/(eB^2).`
A uniform magnetic field of magnitude 0.20 T exists in space from east to west. With what speed should a particle of mass 0.010 g and with charge 1.0 × 10−5 C be projected from south to north so that it moves with uniform velocity?
A particle with a charge of 5.0 µC and a mass of 5.0 × 10−12 kg is projected with a speed of 1.0 km s−1 in a magnetic field of magnitude 5.0 mT. The angle between the magnetic field and the velocity is sin−1 (0.90). Show that the path of the particle will be a helix. Find the diameter of the helix and its pitch.
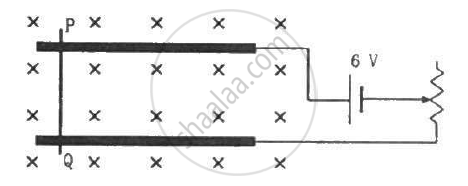
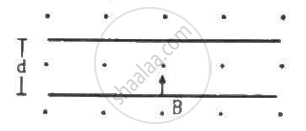
An electron is emitted with negligible speed from the negative plate of a parallel-plate capacitor charged to a potential difference V. The separation between the plates is dand a magnetic field B exists in the space, as shown in the figure. Show that the electron will fail to strike the upper plates if `d > ((2m_eV)/(eB_0^2))^(1/2)`
Current flows through uniform, square frames as shown in the figure. In which case is the magnetic field at the centre of the frame not zero?
