Advertisements
Advertisements
प्रश्न
A particle of mass m and charge q is projected into a region that has a perpendicular magnetic field B. Find the angle of deviation (figure) of the particle as it comes out of the magnetic field if the width d of the region is very slightly smaller than
(a) `(mv)/(qB)` (b)`(mv)/(2qB)` (c)`(2mv)/(qB)`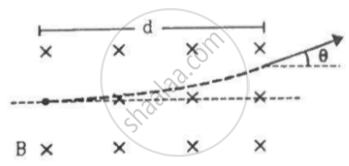
उत्तर
Given:
Mass of the particle = m
Charge of the particle = q
Magnetic field = B
As per the question, the particle is projected into a perpendicular magnetic field.
(a) When the width, d = `(mv)/(qB)`
d is equal to the radius and θ is the angle between the radius and tangent, which is equal to `pi/2`.
(b) When the width, d = `(mv)/(2qB)`
Width of the region in which a magnetic field is applied is half of the radius of the circular path described by the particle.
As the magnetic force is acting only along the y direction, the velocity of the particle will remain constant along the x direction. So, if d is the distance travelled along the x axis, then
d = vxt
`t = (d)/(V_x)`.........(i))
(i)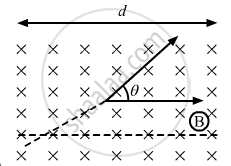
(ii)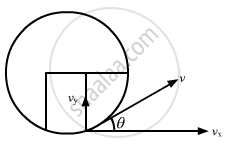
The acceleration along the x direction is zero. The force will act only along the y direction.
Using the equation of motion for motion along the y axis:
vy = uy + ayt
`vy = 0 + (qu_xBt)/(m)`
`= (qu_xBt)/m`
Putting the value of t from equation (i), we get:
`(qu_xBd)/(mv_x)`
we know
`tantheta = (vy)/(vx)`
`(qBd)/(mv_x) = (qBmv_x)/(2qBmvx) = 1/2`
`⇒theta = tan^-1(1/2)`
`= 26.4 = 30^circ = pi/6`
(c) When the width, d = (c) When the width, d = `(2mv)/(qB)`
APPEARS IN
संबंधित प्रश्न
A neutron, an electron and an alpha particle, moving with equal velocities, enter a uniform magnetic field going into the plane of the paper, as shown. Trace their paths in the field and justify your answer.
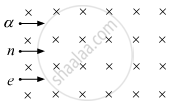
A moving charged particle q travelling along the positive x-axis enters a uniform magnetic field B.
When will the force acting on q be maximum?
A proton and a deuteron having equal momenta enter in a region of a uniform magnetic field at right angle to the direction of a the field. Depict their trajectories in the field.
Write the expression for Lorentz magnetic force on a particle of charge ‘q’ moving with velocity `vecv` in a magnetic field`vecB`. Show that no work is done by this force on the charged particle.
Assume that the magnetic field is uniform in a cubical region and zero outside. Can you project a charged particle from outside into the field, so that the particle describes a complete circle in the field?
An electric current i enters and leaves a uniform circular wire of radius a through diametrically opposite points. A charged particle q, moving along the axis of the circular wire, passes through its centre at speed v. The magnetic force acting on the particle, when it passes through the centre, has a magnitude equal to
If a charged particle at rest experiences no electromagnetic force,
(a) the electric field must be zero
(b) the magnetic field must be zero
(c) the electric field may or may not be zero
(d) the magnetic field may or may not be zero
If a charged particle projected in a gravity-free room deflects,
(a) there must be an electric field
(b) there must be a magnetic field
(c) both fields cannot be zero
(d) both fields can be non-zero
Two particles X and Y having equal charge, after being accelerated through the same potential difference enter a region of uniform magnetic field and describe circular paths of radii R1 and R2 respectively. The ratio of the mass of X to that of Y is ______.
An experimenter's diary reads as follows: "A charged particle is projected in a magnetic field of `(7.0 vec i - 3.0 vecj)xx 10^-3 `T. The acceleration of the particle is found to be `(x veci + 7.0 vecj )` The number to the left of i in the last expression was not readable. What can this number be?
A magnetic field of strength 1.0 T is produced by a strong electromagnet in a cylindrical region of radius 4.0 cm, as shown in the figure. A wire, carrying a current of 2.0 A, is placed perpendicular to and intersecting the axis of the cylindrical region. Find the magnitude of the force acting on the wire.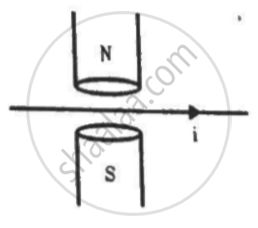
A particle of charge 2.0 × 10−8 C and mass 2.0 × 10−10 g is projected with a speed of 2.0 × 103 m s−1 in a region with a uniform magnetic field of 0.10 T. The velocity is perpendicular to the field. Find the radius of the circle formed by the particle and also the time period.
A proton describes a circle of radius 1 cm in a magnetic field of strength 0.10 T. What would be the radius of the circle described by an α-particle moving with the same speed in the same magnetic field?
An electron of kinetic energy 100 eV circulates in a path of radius 10 cm in a magnetic field. Find the magnetic field and the number of revolutions per second made by the electron.
A particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B, as shown in the figure. (a) Find the radius of the circular arc it describes in the magnetic field. (b) Find the angle subtended by the arc at the centre. (c) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.
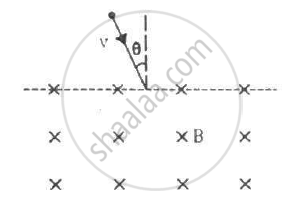
An electron is emitted with negligible speed from the negative plate of a parallel-plate capacitor charged to a potential difference V. The separation between the plates is dand a magnetic field B exists in the space, as shown in the figure. Show that the electron will fail to strike the upper plates if `d > ((2m_eV)/(eB_0^2))^(1/2)`
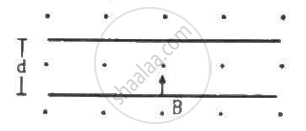
A particle of mass 10 mg and having a charge of 50 mC is projected with a speed of 15 m/s into a uniform magnetic field of 125 mT. Assuming that the particle is projected with its velocity perpendicular to the magnetic field, the time after which the particle reaches its original position for the first time is ______.
