Advertisements
Advertisements
प्रश्न
\[\ce{Fe+}\] ions are accelerated through a potential difference of 500 V and are injected normally into a homogeneous magnetic field B of strength 20.0 mT. Find the radius of the circular paths followed by the isotopes with mass numbers 57 and 58. Take the mass of an ion = A (1.6 × 10−27) kg, where A is the mass number.
उत्तर
Given:
Potential difference through which the Fe+ ions are accelerated, V = 500 V
Strength of the homogeneous magnetic field, B = 20.0 mT = 20 × 10−3 T
Mass numbers of the two isotopes are 57 and 58.
Mass of an ion = A (1.6 × 10−27) kg
We know that the radius of the circular path described by a particle in a magnetic field,
`r = (mv)/(qB)`
For isotope 1,
`r_1= (m_1v_1)/(qB)`
For isotope 2,
`r_2 = (m_2v_2)/(qB)`
⇒`(r_1)/(r_2)=(m_2v_1)/(m_2v_2)`
As both the isotopes are accelerated via the same potential V, the K.E gained by the two particles will be same.
`qV = 1/2 m_1v_1^2 = 1/2m_2v_2^2`
`(m_1)/(m_2) = (v_1^2)/(v_2^2)`
⇒ `(r_1)/(r_2) = ((m_1)/(m_2))^{3/2}`
Also, r1 = `(mv_1)/(qB)`
= `(m_1 sqrt(2qv)/m_1)/(qB)`
= `1/B sqrt ((2m_1V)/q)`
= `sqrt(1000xx57xx1.6xx10^-27)/sqrt (1.6 xx 10^-19 xx 20xx10^-3)`
= `1.19 xx 10^-2m = 119 cm`
For the second isotope:
`As (r_1)/r_2 = ((m_1)/(m_2))^{3/2}`
`r_2 = ((m_2)/(m_1))^{3/2} r_1`
= `(58/57)3/2 xx 119 cm`
= 120 cm
APPEARS IN
संबंधित प्रश्न
Draw a neat labelled diagram for the construction of 'cyclotron'
State the principle of a cyclotron.
Deduce an expression for the frequency of revolution of a charged particle in a magnetic field and show that it is independent of velocity or energy of the particle.
If a charged particle kept at rest experiences an electromagnetic force,
(a) there must be an electric field
(b) there must be a magnetic field
(c) both fields cannot be zero
(d) both fields can be non-zero
An electron is projected horizontally with a kinetic energy of 10 keV. A magnetic field of strength 1.0 × 10−7 T exists in the vertically upward direction.
(a) Will the electron deflect towards the right or left of its motion?
(b) Calculate the sideways deflection of the electron while travelling through 1 m. Make appropriate approximations.
Consider a 10-cm long portion of a straight wire carrying a current of 10 A placed in a magnetic field of 0.1 T making an angle of 53° with the wire. What magnetic force does the wire experience?
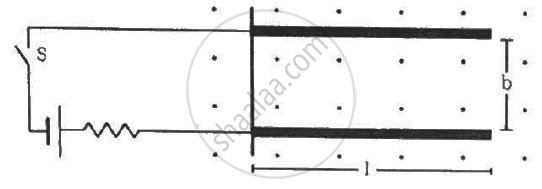
Two metal strips, each of length l, are clamped parallel to each other on a horizontal floor with a separation b between them. A wire of mass m lies on them perpendicularly, as shown in the figure. A vertically-upward magnetic field of strength B exists in the space. The metal strips are smooth but the coefficient of friction between the wire and the floor is µ. A current i is established when the switch S is closed at the instant t = 0. Discuss the motion of the wire after the switch is closed. How far away from the strips will the wire reach?
(a) An electron moves along a circle of radius 1 m in a perpendicular magnetic field of strength 0.50 T. What would be its speed? Is it reasonable? (b) If a proton moves along a circle of the same radius in the same magnetic field, what would be its speed?
Answer the following question.
State the underlying principle of a cyclotron. Explain its working with the help of a schematic diagram. Obtain the expression for cyclotron frequency.
A cyclotron's oscillator frequency is 10 MHz. What should be the operating magnetic field for accelerating protons? If the radius of its 'dees' is 60 cm, calculate the kinetic energy (in MeV) of the proton beam produced by the accelerator.
Cyclotron frequency of a charged particle having charge q and mass m in a cyclotron producing magnetic field B is ______.
Assertion: The frequency of circular motion of a charged particle in cyclotron is independent of the mass of the particle.
Reason: Greater the mass of the particle less will be the frequency of the particle.
An aircraft executes a horizontal loop of radius 1.00 km with a steady speed of 900 km/h. Its centripetal acceleration is ______.
A particle of mass m is moving in a circular path of constant radius r such that, its centripetal acceleration ac is varying with time t as ac = k2rt2, where k is a constant. The power delivered to the particle by the forces acting on it is ______.
The life time of muon in the rest frame is 2 × 10-6 sec. A beam of muons emerges from a cyclotron with velocity where c is the velocity of light The mean life of muons observed in the laboratory frame will be ______.
A cyclotron can accelerate ______.
In a cyclotron, a charged particle ______.
