Advertisements
Advertisements
प्रश्न
Prove that the force acting on a current-carrying wire, joining two fixed points a and b in a uniform magnetic field, is independent of the shape of the wire.
उत्तर
Given:
Uniform magnetic field existing in the region of the wire = B
Let the electric current flowing through the wire be i.
Length of the wire between two points a and b = l
Magnetic force is given by
`vecF = ivecl xx vecB`
`vecF = ilBsinθ`
Let us consider two wires of length l, one straight and the other circular.
The circular wire is of radius a such that `2pia = l`
Suppose the magnetic field is pointing along the z direction and both the wires are lying in the xy plane, so that the angle between the area vector and the magnetic field is 90°.
For the straight wire of length l lying in a uniform magnetic field of strength B :
Force , `F = ilBsin(90^circ) = ilB`
For the circular wire :
Length , `l = 2pia`
Angel between the area vector and magnetic field will again be 90°.
Force acting on the circular wire,
`F = i(2pia)Bsin(90^circ)`
= `i2piaB = ilB`
Both the forces are equal in magnitude. This implies that the magnetic force is independent of the shape of the wire and depends on the length and orientation of the wire.
Therefore, the magnetic force is independent of the shape of the wire.
APPEARS IN
संबंधित प्रश्न
Write the expression, in a vector form, for the Lorentz magnetic force \[\vec{F}\] due to a charge moving with velocity \[\vec{V}\] in a magnetic field \[\vec{B}\]. What is the direction of the magnetic force?
A neutron, an electron and an alpha particle, moving with equal velocities, enter a uniform magnetic field going into the plane of the paper, as shown. Trace their paths in the field and justify your answer.
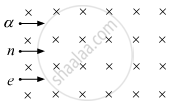
A moving charged particle q travelling along the positive x-axis enters a uniform magnetic field B.
When will the force acting on q be maximum?
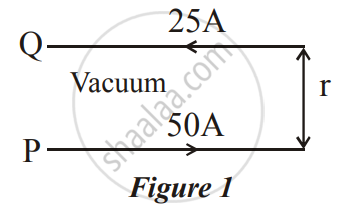
A long horizontal wire P carries a current of 50A. It is rigidly fixed. Another wire Q is placed directly above and parallel to P, as shown in Figure 1 below. The weight per unit length of the wire Q is 0.025 Nm-1 and it carries a current of 25A. Find the distance 'r' of the wire Q from the wire P so that the wire Q remains at rest
A proton and an α-particle move perpendicular to a magnetic field. Find the ratio of radii of circular paths described by them when both have (i) equal velocities, and (ii) equal kinetic energy.
Write the expression for the force,`vecF` acting on a charged particle of charge ‘q’, moving with a velocity `vecV` in the presence of both electric field `vecF`and magnetic field `vecB` . Obtain the condition under which the particle moves undeflected through the fields.
A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one point. If a magnetic field is switched on in the vertical direction, the tension in the string
If a charged particle at rest experiences no electromagnetic force,
(a) the electric field must be zero
(b) the magnetic field must be zero
(c) the electric field may or may not be zero
(d) the magnetic field may or may not be zero
A particle is projected in a plane perpendicular to a uniform magnetic field. The area bounded by the path described by the particle is proportional to
A circular coil of radius 2.0 cm has 500 turns and carries a current of 1.0 A. Its axis makes an angle of 30° with the uniform magnetic field of magnitude 0.40 T that exists in the space. Find the torque acting on the coil.
A square coil of edge l and with n turns carries a current i. It is kept on a smooth horizontal plate. A uniform magnetic field B exists parallel to an edge. The total mass of the coil is M. What should be the minimum value of B for which the coil will start tipping over?
Consider a non-conducting ring of radius r and mass m that has a total charge qdistributed uniformly on it. The ring is rotated about its axis with an angular speed ω. (a) Find the equivalent electric current in the ring. (b) Find the magnetic moment µ of the ring. (c) Show that `pi = (q)/(2m)` l, where l is the angular momentum of the ring about its axis of rotation.
A charged particle is accelerated through a potential difference of 12 kV and acquires a speed of 1.0 × 106 m s−1. It is then injected perpendicularly into a magnetic field of strength 0.2 T. Find the radius of the circle described by it.
A particle of mass m and charge q is projected into a region that has a perpendicular magnetic field B. Find the angle of deviation (figure) of the particle as it comes out of the magnetic field if the width d of the region is very slightly smaller than
(a) `(mv)/(qB)` (b)`(mv)/(2qB)` (c)`(2mv)/(qB)`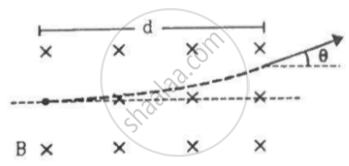
A narrow beam of singly-charged carbon ions, moving at a constant velocity of 6.0 × 104m s−1, is sent perpendicularly in a rectangular region of uniform magnetic field B = 0.5 T (figure). It is found that two beams emerge from the field in the backward direction, the separations from the incident beam being 3.0 cm and 3.5 cm. Identify the isotopes present in the ion beam. Take the mass of an ion = A(1.6 × 10−27) kg, where A is the mass number.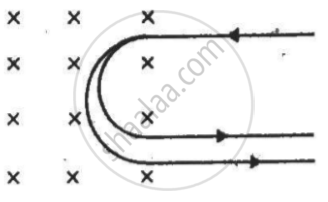
A narrow beam of singly charged potassium ions of kinetic energy 32 keV is injected into a region of width 1.00 cm with a magnetic field of strength 0.500 T, as shown in the figure. The ions are collected at a screen 95.5 cm away from the field region. If the beam contains isotopes of atomic weights 39 and 41, find the separation between the points where these isotopes strike the screen. Take the mass of a potassium ion = A (1.6 × 10−27) kg, where A is the mass number.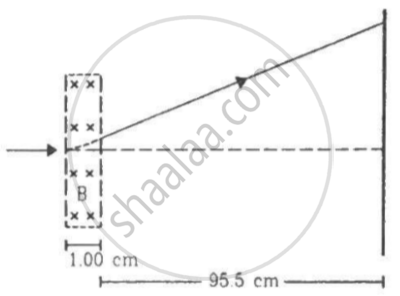
Doubly-ionised helium ions are projected with a speed of 10 km s−1 in a direction perpendicular to a uniform magnetic field of magnitude 1.0 T. Find (a) the force acting on an ion (b) the radius of the circle in which it circulates and (c) the time taken by an ion to complete the circle.
A particle of mass m and charge q is released from the origin in a region in which the electric field and magnetic field are given by
`vecB = -B_0 vecj and vecE = E_0 vecK `
Find the speed of the particle as a function of its z-coordinate.
When does a moving charged particle nor experience any force while moving through a uniform magnetic field?
