Advertisements
Advertisements
प्रश्न
A current loop of arbitrary shape lies in a uniform magnetic field B. Show that the net magnetic force acting on the loop is zero.
उत्तर
Given:
Uniform magnetic field existing in the region of the arbitrary loop = B
Let the electric current flowing through the loop be i.
Length of each side of the loop is l.
Assume that the direction of the current is clockwise.
Direction of the magnetic field is going into the plane of the loop.
Magnetic force is given by
`vecF = i veclxxvecB`
`vecF = ilBsintheta`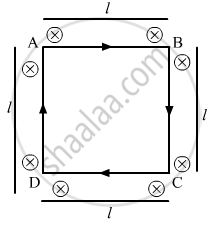
Here, θ = 90˚
Direction of force can be found using Fleming's lef- hand rule.
Force F1 acting on AB = ilB upwards
Force F2 acting on DC = ilB downwards
So, F1 and F2 cancel each other.
Force F3 acting on AD = ilB outwards (Pointing towards the left from AB)
Force F4 acting on BC = ilB outwards (Pointing towards the right from BC)
So, F3 and F4 cancel each other.
Therefore, the net force acting on the arbitrary loop is 0.
APPEARS IN
संबंधित प्रश्न
Draw a neat and labelled diagram of suspended coil type moving coil galvanometer.
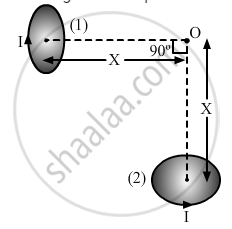
Two very small identical circular loops, (1) and (2), carrying equal currents I are placed vertically (with respect to the plane of the paper) with their geometrical axes perpendicular to each other as shown in the figure. Find the magnitude and direction of the net magnetic field produced at the point O.
Two identical circular loops, P and Q, each of radius r and carrying equal currents are
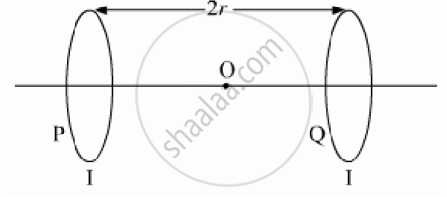
kept in the parallel planes having a common axis passing through O. The direction of current in P is clockwise and in Q is anti-clockwise as seen from O which is equidistant from the loops P and Q. Find the magnitude of the net magnetic field at O.
Write the expression for the magnetic moment `vecm`due to a planar square loop of side ‘l’ carrying a steady current I in a vector form.
In the given figure this loop is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance l as shown. Give reason to explain that the loop will experience a net force but no torque. Write the expression for this force acting on the loop.

Is it possible for a current loop to stay without rotating in a uniform magnetic field? If yes, what should be the orientation of the loop?
A rectangular wire-loop of width a is suspended from the insulated pan of a spring balance, as shown in the figure. A current i exists in the anti-clockwise direction in the loop. A magnetic field B exists in the lower region. Find the change in the tension of the spring if the current in the loop is reversed.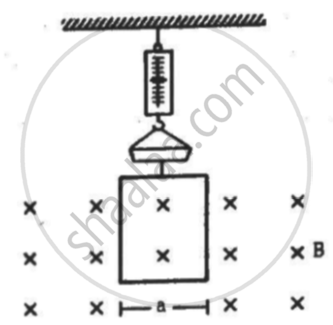
Suppose that the radius of cross-section of the wire used in the previous problem is r. Find the increase in the radius of the loop if the magnetic field is switched off. Young's modulus of the material of the wire is Y.
A moving coil galvanometer has been fitted with a rectangular coil having 50 turns and dimensions 5 cm × 3 cm. The radial magnetic field in which the coil is suspended is of 0.05 Wb/m2. The torsional constant of the spring is 1.5 × 10−9 Nm/degree. Obtain the current required to be passed through the galvanometer so as to produce a deflection of 30°.
Derive an expression for the net torque on a rectangular current carrying loop placed in a uniform magnetic field with its rotational axis perpendicular to the field.
A rectangular coil of length 0.12 m and width 0.1 m having 100 turns of wire is suspended vertically in a uniform magnetic field of strength 0.4 Wb/m2. The coil carries a current of 2.5 A. If the plane of the coil is inclined at an angle of 30° with the direction of the field, the torque required to keep the coil in stable equilibrium will be ____________.
Torque acting on a rectangular coil carrying current 'l' situated parallel to magnetic field of induction 'B', having number of turns 'n' and area 'A' is ______.
A rectangular coil has 200 turns each of area 50 cm2 . It is capable of rotation about an axis joining the mid points of two opposite sides. When a current of 10 A is passed through it while its plane is at right angles to a uniform magnetic field, it experiences a torque of 5 Nm. The magnetic field will be ____________.
If number of turns in moving coil galvanometer becomes half, then the deflection for the same current will become ____________.
The current flowing through moving coil galvanometer is 20% of the current to be measured. The resistance of moving coil galvanometer is 48 `Omega`, then shunt required is ____________.
An ammeter is obtained by shunting 'n' `Omega` galvanometer with 'n' `Omega` resistance. The additional shunt required to be connected across it to double the range is ____________.
A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the
(a) total torque on the coil,
(b) total force on the coil,
(c) average force on each electron in the coil due to the magnetic field?
(The coil is made of copper wire of cross-sectional area 10–5 m2, and the free electron density in copper is given to be about 1029 m–3.)
When the plane of the coil is parallel to the field, torque will be ______
A current of 10 A is flowing in a wire of length 1.5 m. A force of 15 N acts on it when it is placed in a uniform magnetic field of 2 T. The angle between the magnetic field and the direction of the current is ______.
Equal current i flows in two segments of a circular loop in the direction shown in figure. Radius of the loop is r. The magnitude of magnetic field induction at the centre of the loop is ______.
A rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a radial magnetic field of 0.01 T. If the torsional constant of the suspension fibre is 5 × 10−9 N·m per degree, find the angle through which the coil rotates when a current of 30 μA is passed through it.
