Advertisements
Advertisements
Question
Prove that the force acting on a current-carrying wire, joining two fixed points a and b in a uniform magnetic field, is independent of the shape of the wire.
Solution
Given:
Uniform magnetic field existing in the region of the wire = B
Let the electric current flowing through the wire be i.
Length of the wire between two points a and b = l
Magnetic force is given by
`vecF = ivecl xx vecB`
`vecF = ilBsinθ`
Let us consider two wires of length l, one straight and the other circular.
The circular wire is of radius a such that `2pia = l`
Suppose the magnetic field is pointing along the z direction and both the wires are lying in the xy plane, so that the angle between the area vector and the magnetic field is 90°.
For the straight wire of length l lying in a uniform magnetic field of strength B :
Force , `F = ilBsin(90^circ) = ilB`
For the circular wire :
Length , `l = 2pia`
Angel between the area vector and magnetic field will again be 90°.
Force acting on the circular wire,
`F = i(2pia)Bsin(90^circ)`
= `i2piaB = ilB`
Both the forces are equal in magnitude. This implies that the magnetic force is independent of the shape of the wire and depends on the length and orientation of the wire.
Therefore, the magnetic force is independent of the shape of the wire.
APPEARS IN
RELATED QUESTIONS
An electron moving horizontally with a velocity of 4 ✕ 104 m/s enters a region of uniform magnetic field of 10−5 T acting vertically upward as shown in the figure. Draw its trajectory and find out the time it takes to come out of the region of magnetic
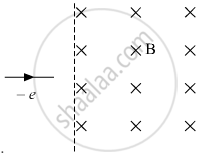
field.
A proton and a deuteron having equal momenta enter in a region of a uniform magnetic field at right angle to the direction of a the field. Depict their trajectories in the field.
Write the expression for Lorentz magnetic force on a particle of charge ‘q’ moving with velocity `vecv` in a magnetic field`vecB`. Show that no work is done by this force on the charged particle.
A positively-charged particle projected towards east is deflected towards north by a magnetic field. The field may be
A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one point. If a magnetic field is switched on in the vertical direction, the tension in the string
A charged particle moves in a gravity-free space without change in velocity. Which of the following is/are possible?
(a) E = 0, B = 0
(b) E = 0, B ≠ 0
(c) E ≠ 0, B = 0
(d) E ≠ 0, B ≠ 0
Two ions have equal masses but one is singly-ionised and the other is doubly-ionised. They are projected from the same place in a uniform magnetic field with the same velocity perpendicular to the field.
(a) Both ions will move along circles of equal radii.
(b) The circle described by the singly-ionised charge will have a radius that is double that of the other circle.
(c) The two circles do not touch each other.
(d) The two circles touch each other.
A particle is projected in a plane perpendicular to a uniform magnetic field. The area bounded by the path described by the particle is proportional to
A current of 2 A enters at the corner d of a square frame abcd of side 20 cm and leaves at the opposite corner b. A magnetic field B = 0.1 T exists in the space in a direction perpendicular to the plane of the frame, as shown in the figure. Find the magnitude and direction of the magnetic forces on the four sides of the frame.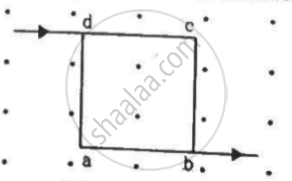
A magnetic field of strength 1.0 T is produced by a strong electromagnet in a cylindrical region of radius 4.0 cm, as shown in the figure. A wire, carrying a current of 2.0 A, is placed perpendicular to and intersecting the axis of the cylindrical region. Find the magnitude of the force acting on the wire.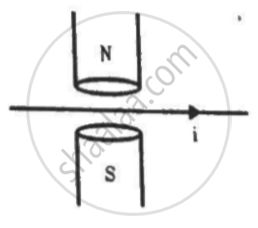
A wire, carrying a current i, is kept in the x−y plane along the curve y = A sin `((2x)/lamda x)`. magnetic field B exists in the z direction. Find the magnitude of the magnetic force on the portion of the wire between x = 0 and x = λ.
Protons with kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field, so that it just misses a plane target kept at a distance l in front of the accelerator. Find the magnetic field.
A particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B, as shown in the figure. (a) Find the radius of the circular arc it describes in the magnetic field. (b) Find the angle subtended by the arc at the centre. (c) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.
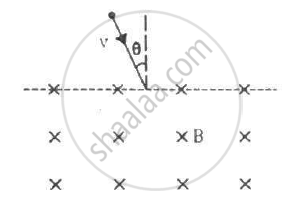
A uniform magnetic field of magnitude 0.20 T exists in space from east to west. With what speed should a particle of mass 0.010 g and with charge 1.0 × 10−5 C be projected from south to north so that it moves with uniform velocity?
A particle moves in a circle of diameter 1.0 cm under the action of a magnetic field of 0.40 T. An electric field of 200 V m−1 makes the path straight. Find the charge/mass ratio of the particle.
Current flows through uniform, square frames as shown in the figure. In which case is the magnetic field at the centre of the frame not zero?
The velocity of a body of mass 2 kg as a function of time t is given by v(t) = 2t`hat"i" + "t"^2hat"j"`. The force acting on it, at time t = 2 s is given by ______.
