Advertisements
Advertisements
Question
An electron moving horizontally with a velocity of 4 ✕ 104 m/s enters a region of uniform magnetic field of 10−5 T acting vertically upward as shown in the figure. Draw its trajectory and find out the time it takes to come out of the region of magnetic
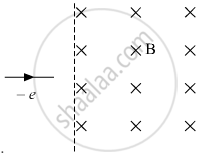
field.
Solution
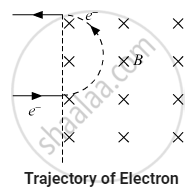
Let the time taken by the electron to come out of the region of magnetic field be t.
Velocity of the electron, v = 4 × 104 m/s
Magnetic field, B = 10−5 T
Mass of the electron, m = 9 × 10−31 kg
We know
\[t = \frac{\pi r}{v}\]
\[\text { where r } = \frac{mv}{Bq}\]
\[\text { Now,} \]
\[t = \frac{\pi m}{Bq} = \frac{3 . 14 \times 9 \times {10}^{- 31}}{{10}^{- 5} \times 1 . 6 \times {10}^{- 19}}\]
\[ \Rightarrow t = 17 . 66 \times {10}^{- 7} s = 1 . 76 \mu s\]
Thus, the time taken by the electron to come out of the region of magnetic field is 1.76 μs.
APPEARS IN
RELATED QUESTIONS
Write the expression, in a vector form, for the Lorentz magnetic force \[\vec{F}\] due to a charge moving with velocity \[\vec{V}\] in a magnetic field \[\vec{B}\]. What is the direction of the magnetic force?
A proton and an α-particle move perpendicular to a magnetic field. Find the ratio of radii of circular paths described by them when both have (i) equal velocities, and (ii) equal kinetic energy.
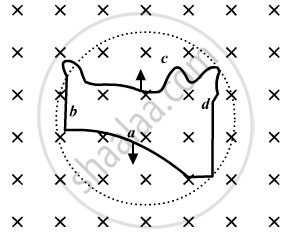
A flexible wire of irregular shape, abcd, as shown in the figure, turns into a circular shape when placed in a region of magnetic field which is directed normal to the plane of the loop away from the reader. Predict the direction of the induced current in the wire.
Write the expression for Lorentz magnetic force on a particle of charge ‘q’ moving with velocity `vecv` in a magnetic field`vecB`. Show that no work is done by this force on the charged particle.
A magnetic field of \[(4.0\times10^-3 \overrightarrow k)\] T exerts a force of \[(4.0 \overrightarrow i + 3.0 \overrightarrow j ) \times 10^{−10} N\] on a particle with a charge of 1.0 × 10−9 C and going in the x − y plane. Find the velocity of the particle.
Consider three quantities \[x = E/B, y = \sqrt{1/ \mu_0 \epsilon_0}\] and \[z = \frac{l}{CR}\] . Here, l is the length of a wire, C is a capacitance and R is a resistance. All other symbols have standard meanings.
(a) x, y have the same dimensions.
(b) y, z have the same dimensions.
(c) z, x have the same dimensions.
(d) None of the three pairs have the same dimensions.
A wire, carrying a current i, is kept in the x−y plane along the curve y = A sin `((2x)/lamda x)`. magnetic field B exists in the z direction. Find the magnitude of the magnetic force on the portion of the wire between x = 0 and x = λ.
Protons with kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field, so that it just misses a plane target kept at a distance l in front of the accelerator. Find the magnetic field.
When does a moving charged particle nor experience any force while moving through a uniform magnetic field?
