Advertisements
Advertisements
Question
Three point charges +q each are kept at the vertices of an equilateral triangle of side 'l'. Determine the magnitude and sign of the charge to be kept at its centroid so that the charges at the vertices remain in equilibrium.
Solution

Let the charge at the centroid of the triangle ABC be Q.
The system will be in equilibrium if the net force on all the charges is zero.
In the given equilateral triangle ABC of sides of length l, if we draw a perpendicular AM to the side BC, then we get
\[AM = ACcos {30}^o = \frac{\sqrt{3}}{2}l\]
\[AG = \frac{2}{3}AD = \frac{1}{\sqrt{3}}l\]
By symmetry, AG = BG = CG.
Also, the net force on charge Q is zero.
Now, let us calculate the force on the charge placed at vertex B.
\[\vec{F}_{net} = \vec{F}_C + \vec{F}_A + \vec{F}_G \]
\[ \vec{F}_C =\frac{q^2}{4\pi \epsilon_0 l^2}\left( - \vec{i} \right) . . . . . \left( i \right)\]
\[ \vec{F}_A = \frac{q^2}{4\pi \epsilon_0 l^2}\left( \left( - \cos {60}^o \right) \vec {i}+ \left( - \sin {60}^o \right) \vec{j} \right) . . . . . \left( ii \right)\]
\[ \vec{F}_G = \frac{qQ}{4\pi\epsilon_0 \left( \frac{l}{\sqrt{3}} \right)^2} \left( \left( - \cos {30}^o \right)\vec{i} + \left( - \sin {30}^o \right) \vec{j} \right) . . . . . \left( iii \right)\]
\[\text { Adding }\left( i \right), \left( ii \right) \text { and } \left( iii \right), \text { we get }\]
\[ \vec{F}_{net} = \frac{q}{4\pi \epsilon_0 l^2}\left[ \left( - q - \frac{q}{2} - \frac{3\sqrt{3}Q}{2} \right) \vec{i} + \left( - \frac{\sqrt{3}q}{2} - \frac{3Q}{2} \right) \vec{j} \right]\]
\[\text { For equilibrium, net} = 0 . \]
\[\text { So }, \]
\[\left( - q - \frac{q}{2} - \frac{3\sqrt{3}Q}{2} \right) = 0 \text { and } \left( - \frac{\sqrt{3}q}{2} - \frac{3Q}{2} \right) = 0\]
\[ \Rightarrow Q = - \frac{q}{\sqrt{3}}\]
APPEARS IN
RELATED QUESTIONS
What is the work done by the field of a nucleus in a complete circular orbit of the electron? What if the orbit is elliptical?
We know that electric field is discontinuous across the surface of a charged conductor. Is electric potential also discontinuous there?
Obtain an expression for an intensity of electric field at a point at the end of position, i.e., the axial position of an electric dipole.
x
Why must electrostatic field be normal to the surface at every point of a charged conductor?
The electrostatic potential energy of two-point charges, 1 µC each, placed 1 meter apart in the air is:
A work of 100 joule is performed in carrying a charge of 5 coulomb form infinity to a particular. point in an' electrostatic field. The potential of this point is:-
Potential energy of two equal negative point charges 2µc each held lm apart in air is:-
In bringing one electron towards another electrons, the electrostatic potential energy of the system will.
When one electron is taken towards the other electron, then the electric potential energy of the system ______
Three-point charges Q, q and -q are kept at the vertices of an equilateral triangle of side L as shown in the figure. What is
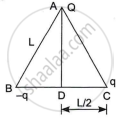
- the electrostatic potential energy of the arrangement? and
- the potential at point D?
