Advertisements
Advertisements
Question
Four charges +q, −q, +q and −q are to be arranged respectively at the four corners of a square ABCD of side 'a'.
(a) Find the work required to put together this arrangement.
(b) A charge q0 is brought to the centre of the square, the four charges being held fixed. How much extra work is needed to do this ?
Solution
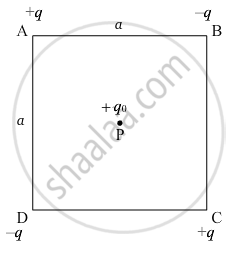
Here,
AB = BC = CD = DA = a
And,
\[AC = BD = a\sqrt{2}\]
Now,
\[\text{ Total work done} \left( W \right) = \text { Potential energy of the system of four charges } \]
\[W = \frac{\left( - q \right)\left( + q \right)}{4 \pi\epsilon_0 a} + \frac{\left( + q \right)\left( - q \right)}{4 \pi\epsilon_0 a} + \frac{\left( - q \right)\left( + q \right)}{4 \pi\epsilon_0 a} + \frac{\left( + q \right)\left( - q \right)}{4 \pi\epsilon_0 a} + \frac{1}{4 \pi\epsilon_0}\frac{\left( \left( - q \right)\left( - q \right) \right)}{a\sqrt{2}} + \frac{1}{4 \pi\epsilon_0}\frac{\left( \left( + q \right)\left( + q \right) \right)}{a\sqrt{2}}\]
\[ = \frac{- 4 q^2}{4 \pi\epsilon_0 a} + \frac{2 q^2}{4 \pi\epsilon_0 a\sqrt{2}} = \frac{- q^2}{4 \pi\epsilon_0 a}\left( 4 - \sqrt{2} \right)\]
\[\left( b \right)\]
\[\text { Extra work needed,} W_P = q_0 \times V_P \]
\[\text { Here,} \]
\[V_P \text{= Potential at point P }\]
\[\text { Now,} \]
\[\text { Potential at point P } = \frac{q}{4\pi \epsilon_0 \frac{a\sqrt{2}}{2}} + \frac{\left( - q \right)}{4\pi \epsilon_0 \frac{a\sqrt{2}}{2}} + \frac{q}{4\pi \epsilon_0 \frac{a\sqrt{2}}{2}} + \frac{\left( - q \right)}{4\pi \epsilon_0 \frac{a\sqrt{2}}{2}} = 0\]
\[ \Rightarrow W = 0\]
APPEARS IN
RELATED QUESTIONS
A particle of mass m and charge (−q) enters the region between the two charged plates initially moving along x-axis with speed vx (like particle 1 in the fig.). The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL2/(2m`"v"_"x"^2`).

Two identical pith balls, each carrying a charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
A particle A with a charge of 2.0 × 10−6 C and a mass of 100 g is placed at the bottom of a smooth inclined plane of inclination 30°. Where should another particle B, with the same charge and mass, be placed on the incline so that it may remain in equilibrium?
Repeat the previous problem if the particle C is displaced through a distance x along the line AB.
Two charged particles, with equal charges of 2.0 × 10−5 C, are brought from infinity to within a separation of 10 cm. Find the increase in the electric potential energy during the process
Two identical particles, each with a charge of 2.0 × 10−4 C and mass of 10 g, are kept at a separation of 10 cm and then released. What would be the speed of the particles when the separation becomes large?
Write down Coulomb’s law in vector form and mention what each term represents.
Write a short note on superposition principle.
A total charge Q is broken in two parts Q1 and Q2 and they are placed at a distance R from each other. The maximum force of repulsion between them will occur, when ____________.
