Advertisements
Advertisements
प्रश्न
Four charges +q, −q, +q and −q are to be arranged respectively at the four corners of a square ABCD of side 'a'.
(a) Find the work required to put together this arrangement.
(b) A charge q0 is brought to the centre of the square, the four charges being held fixed. How much extra work is needed to do this ?
उत्तर
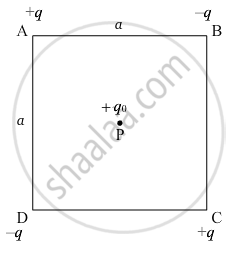
Here,
AB = BC = CD = DA = a
And,
\[AC = BD = a\sqrt{2}\]
Now,
\[\text{ Total work done} \left( W \right) = \text { Potential energy of the system of four charges } \]
\[W = \frac{\left( - q \right)\left( + q \right)}{4 \pi\epsilon_0 a} + \frac{\left( + q \right)\left( - q \right)}{4 \pi\epsilon_0 a} + \frac{\left( - q \right)\left( + q \right)}{4 \pi\epsilon_0 a} + \frac{\left( + q \right)\left( - q \right)}{4 \pi\epsilon_0 a} + \frac{1}{4 \pi\epsilon_0}\frac{\left( \left( - q \right)\left( - q \right) \right)}{a\sqrt{2}} + \frac{1}{4 \pi\epsilon_0}\frac{\left( \left( + q \right)\left( + q \right) \right)}{a\sqrt{2}}\]
\[ = \frac{- 4 q^2}{4 \pi\epsilon_0 a} + \frac{2 q^2}{4 \pi\epsilon_0 a\sqrt{2}} = \frac{- q^2}{4 \pi\epsilon_0 a}\left( 4 - \sqrt{2} \right)\]
\[\left( b \right)\]
\[\text { Extra work needed,} W_P = q_0 \times V_P \]
\[\text { Here,} \]
\[V_P \text{= Potential at point P }\]
\[\text { Now,} \]
\[\text { Potential at point P } = \frac{q}{4\pi \epsilon_0 \frac{a\sqrt{2}}{2}} + \frac{\left( - q \right)}{4\pi \epsilon_0 \frac{a\sqrt{2}}{2}} + \frac{q}{4\pi \epsilon_0 \frac{a\sqrt{2}}{2}} + \frac{\left( - q \right)}{4\pi \epsilon_0 \frac{a\sqrt{2}}{2}} = 0\]
\[ \Rightarrow W = 0\]
APPEARS IN
संबंधित प्रश्न
Find the electric force between two protons separated by a distance of 1 fermi (1 fermi = 10−15 m). The protons in a nucleus remain at a separation of this order.
Suppose all the electrons of 100 g water are lumped together to form a negatively-charged particle and all the nuclei are lumped together to form a positively-charged particle. If these two particles are placed 10.0 cm away from each other, find the force of attraction between them. Compare it with your weight.
Two charged particles with charge 2.0 × 10−8 C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
Repeat the previous problem if the particle C is displaced through a distance x along the line AB.
Two charged particles, with equal charges of 2.0 × 10−5 C, are brought from infinity to within a separation of 10 cm. Find the increase in the electric potential energy during the process
Coulomb's law is given by F = k q1q2 rn where n is
The S.I unit of electric permittivity is
Which of the following statements about nuclear forces is not true?
What is meant by the statement: "Relative permittivity of water is 81"?
