Advertisements
Advertisements
Question
Repeat the previous problem if the particle C is displaced through a distance x along the line AB.
Solution
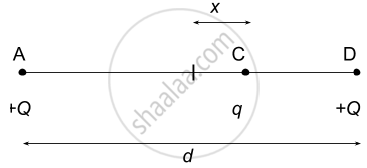Net force
\[= \frac{1}{4\pi \in_0}\left[ \frac{Qq}{\left( \frac{d}{2} - x \right)^2} - \frac{Qq}{\left( \frac{d}{2} + x \right)^2} \right]\]
\[ = \frac{Qq}{4\pi \in_0}\frac{\left[ \left( \frac{d}{2} \right)^2 + x^2 + xd - \left( \frac{d}{2} \right)^2 - x^2 + xd \right]}{\left[ \left( \frac{d}{2} \right)^2 - x^2 \right]^2}\]
when,
x << d
So, net force = \[\frac{qQ}{4\pi \in_0}\frac{\left( 2xd \right)}{d^4}\]
\[ = \frac{qQ}{4\pi \in_0}\frac{2x}{d^3}\]
\[\text{ Or m }\left( \frac{2\pi}{T} \right)^2 x = \frac{2xqQ}{4\pi \in_0 d^3}\]
\[T = \left[ \frac{\pi^3 \in_0 m d^3}{2Qq} \right]^{1/2}\]
APPEARS IN
RELATED QUESTIONS
The electrostatic force on a small sphere of charge 0.4 μC due to another small sphere of charge − 0.8 μC in air is 0.2 N.
- What is the distance between the two spheres?
- What is the force on the second sphere due to the first?
At what separation should two equal charges, 1.0 C each, be placed, so that the force between them equals the weight of a 50 kg person?
Two charges 2.0 × 10−6 C and 1.0 × 10−6 C are placed at a separation of 10 cm. Where should a third charge be placed, such that it experiences no net force due to these charges?
Consider a gold nucleus to be a sphere of radius 6.9 fermi in which protons and neutrons are distributed. Find the force of repulsion between two protons situated at largest separation. Why do these protons not fly apart under this repulsion?
NaCl molecule is bound due to the electric force between the sodium and the chlorine ions when one electron of sodium is transferred to chlorine. Taking the separation between the ions to be 2.75 × 10−8 cm, find the force of attraction between them. State the assumptions (if any) that you have made.
Three equal charges, 2.0 × 10−6 C each, are held at the three corners of an equilateral triangle of side 5 cm. Find the Coulomb force experienced by one of the charges due to the other two.
Two charged particles with charge 2.0 × 10−8 C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
Two identical balls, each with a charge of 2.00 × 10−7 C and a mass of 100 g, are suspended from a common point by two insulating strings, each 50 cm long. The balls are held at a separation 5.0 cm apart and then released. Find.
(a) the electric force on one of the charged balls
(b) the components of the resultant force on it along and perpendicular to the string
(c) the tension in the string
(d) the acceleration of one of the balls. Answers are to be obtained only for the instant just after the release.
Two identically-charged particles are fastened to the two ends of a spring of spring constant 100 N m−1 and natural length 10 cm. The system rests on a smooth horizontal table. If the charge on each particle is 2.0 × 10−8 C, find the extension in the length of the spring. Assume that the extension is small as compared to the natural length. Justify this assumption after you solve the problem.
Answer the following question.
What is relative permittivity?
Solve numerical example.
Three equal charges of 10×10-8 C respectively, each located at the corners of a right triangle whose sides are 15 cm, 20 cm, and 25cm respectively. Find the force exerted on the charge located at the 90° angle.
Explain in detail Coulomb’s law and its various aspects.
The electric force acting between two point charges kept at a certain distance in vacuum is 16 N. If the same two charges are kept at the same distance in a medium of dielectric constant 8, the electric force acting between them is ____________ N.
Two identical thin rings, each of radius a meter, are coaxially placed at a distance R meter apart. If Q1 coulomb and Q2 coulomb are respectively the charges uniformly spread on the two rings, the work done in moving a charge q coulomb from the centre of one ring to that of the other is ______.
The S.I unit of electric permittivity is
Identify the wrong statement in the following.
Coulomb's law correctly describes the electric force that ______
Two charges q and – 3q are placed fixed on x-axis separated by distance ‘d’. Where should a third charge 2q be placed such that it will not experience any force?
There is another useful system of units, besides the SI/mks A system, called the cgs (centimeter-gram-second) system. In this system Coloumb’s law is given by
F = `(Qq)/r^2 hatr`
where the distance r is measured in cm (= 10–2 m), F in dynes (= 10–5 N) and the charges in electrostatic units (es units), where 1 es unit of charge = `1/([3]) xx 10^-9 C`
The number [3] actually arises from the speed of light in vaccum which is now taken to be exactly given by c = 2.99792458 × 108 m/s. An approximate value of c then is c = [3] × 108 m/s.
(i) Show that the coloumb law in cgs units yields
1 esu of charge = 1 (dyne)1/2 cm.
Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of charge = x C, where x is a dimensionless number. Show that this gives
`1/(4pi ∈_0) = 10^-9/x^2 (N*m^2)/C^2`
With `x = 1/([3]) xx 10^-9`, we have `1/(4pi ∈_0) = [3]^2 xx 10^9 (Nm^2)/C^2`
or, `1/(4pi ∈_0) = (2.99792458)^2 xx 10^9 (Nm^2)/C^2` (exactly).
Which of the following statements about nuclear forces is not true?
What is meant by the statement: "Relative permittivity of water is 81"?
