Advertisements
Advertisements
प्रश्न
Three point charges +q each are kept at the vertices of an equilateral triangle of side 'l'. Determine the magnitude and sign of the charge to be kept at its centroid so that the charges at the vertices remain in equilibrium.
उत्तर

Let the charge at the centroid of the triangle ABC be Q.
The system will be in equilibrium if the net force on all the charges is zero.
In the given equilateral triangle ABC of sides of length l, if we draw a perpendicular AM to the side BC, then we get
\[AM = ACcos {30}^o = \frac{\sqrt{3}}{2}l\]
\[AG = \frac{2}{3}AD = \frac{1}{\sqrt{3}}l\]
By symmetry, AG = BG = CG.
Also, the net force on charge Q is zero.
Now, let us calculate the force on the charge placed at vertex B.
\[\vec{F}_{net} = \vec{F}_C + \vec{F}_A + \vec{F}_G \]
\[ \vec{F}_C =\frac{q^2}{4\pi \epsilon_0 l^2}\left( - \vec{i} \right) . . . . . \left( i \right)\]
\[ \vec{F}_A = \frac{q^2}{4\pi \epsilon_0 l^2}\left( \left( - \cos {60}^o \right) \vec {i}+ \left( - \sin {60}^o \right) \vec{j} \right) . . . . . \left( ii \right)\]
\[ \vec{F}_G = \frac{qQ}{4\pi\epsilon_0 \left( \frac{l}{\sqrt{3}} \right)^2} \left( \left( - \cos {30}^o \right)\vec{i} + \left( - \sin {30}^o \right) \vec{j} \right) . . . . . \left( iii \right)\]
\[\text { Adding }\left( i \right), \left( ii \right) \text { and } \left( iii \right), \text { we get }\]
\[ \vec{F}_{net} = \frac{q}{4\pi \epsilon_0 l^2}\left[ \left( - q - \frac{q}{2} - \frac{3\sqrt{3}Q}{2} \right) \vec{i} + \left( - \frac{\sqrt{3}q}{2} - \frac{3Q}{2} \right) \vec{j} \right]\]
\[\text { For equilibrium, net} = 0 . \]
\[\text { So }, \]
\[\left( - q - \frac{q}{2} - \frac{3\sqrt{3}Q}{2} \right) = 0 \text { and } \left( - \frac{\sqrt{3}q}{2} - \frac{3Q}{2} \right) = 0\]
\[ \Rightarrow Q = - \frac{q}{\sqrt{3}}\]
APPEARS IN
संबंधित प्रश्न
What is the work done by the field of a nucleus in a complete circular orbit of the electron? What if the orbit is elliptical?
Guess a possible reason why water has a much greater dielectric constant (= 80) than say, mica (= 6).
Three point charges +2, +2, and +5µC are placed respectively at the vertices A, B, C of an equilateral triangle of side 0.2 m. The magnitude of the force experienced by the charge at C is ______.
If stretch in a spring of force constant k is tripled then the ratio of elastic potential energy in the two cases will be:
In bringing one electron towards another electrons, the electrostatic potential energy of the system will.
When one electron is taken towards the other electron, then the electric potential energy of the system ______
In a region of constant potential ______.
- the electric field is uniform
- the electric field is zero
- there can be no charge inside the region
- the electric field shall necessarily change if a charge is placed outside the region
Three-point charges Q, q and -q are kept at the vertices of an equilateral triangle of side L as shown in the figure. What is
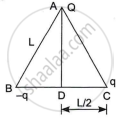
- the electrostatic potential energy of the arrangement? and
- the potential at point D?
