Advertisements
Advertisements
Question
Consider three quantities \[x = E/B, y = \sqrt{1/ \mu_0 \epsilon_0}\] and \[z = \frac{l}{CR}\] . Here, l is the length of a wire, C is a capacitance and R is a resistance. All other symbols have standard meanings.
(a) x, y have the same dimensions.
(b) y, z have the same dimensions.
(c) z, x have the same dimensions.
(d) None of the three pairs have the same dimensions.
Solution
(a) x, y have the same dimensions.
(b) y, z have the same dimensions.
(c) z, x have the same dimensions.
Lorentz Force:
\[qvB = qE\]
\[ \Rightarrow \text{ Dimensions of x }= [v] = \left[ \frac{E}{B} \right] = [ {LT}^{- 1} ]\]
\[y = \frac{1}{\sqrt{\mu_o \epsilon_o}} = \sqrt{\frac{4\pi}{\mu_o} \times \frac{1}{4 \pi\epsilon_o}} = \sqrt{\frac{9 \times {10}^9}{{10}^{- 7}}} = 3 \times {10}^8 = c\]
\[ \Rightarrow \text{ Dimensions of y }= [c] = [ {LT}^{- 1} ]\]
Time constant of RC circuit = RC so dimensionally [RC] = [T]
Therefore, x, y and z have the same dimensions.
APPEARS IN
RELATED QUESTIONS
Write the expression for the force `vecF` acting on a particle of mass m and charge q moving with velocity `vecV` in a magnetic field `vecB` , Under what conditions will it move in (i) a circular path and (ii) a helical path?
A proton and a deuteron having equal momenta enter in a region of a uniform magnetic field at right angle to the direction of a the field. Depict their trajectories in the field.
A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one point. If a magnetic field is switched on in the vertical direction, the tension in the string
A beam consisting of protons and electrons moving at the same speed goes through a thin region in which there is a magnetic field perpendicular to the beam. The protons and the electrons
If a charged particle at rest experiences no electromagnetic force,
(a) the electric field must be zero
(b) the magnetic field must be zero
(c) the electric field may or may not be zero
(d) the magnetic field may or may not be zero
A magnetic field of \[(4.0\times10^-3 \overrightarrow k)\] T exerts a force of \[(4.0 \overrightarrow i + 3.0 \overrightarrow j ) \times 10^{−10} N\] on a particle with a charge of 1.0 × 10−9 C and going in the x − y plane. Find the velocity of the particle.
An experimenter's diary reads as follows: "A charged particle is projected in a magnetic field of `(7.0 vec i - 3.0 vecj)xx 10^-3 `T. The acceleration of the particle is found to be `(x veci + 7.0 vecj )` The number to the left of i in the last expression was not readable. What can this number be?
A 10 g bullet with a charge of 4.00 μC is fired at a speed of 270 m s−1 in a horizontal direction. A vertical magnetic field of 500 µT exists in the space. Find the deflection of the bullet due to the magnetic field as it travels through 100 m. Make appropriate approximations.
Prove that the force acting on a current-carrying wire, joining two fixed points a and b in a uniform magnetic field, is independent of the shape of the wire.
A semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
A particle of charge 2.0 × 10−8 C and mass 2.0 × 10−10 g is projected with a speed of 2.0 × 103 m s−1 in a region with a uniform magnetic field of 0.10 T. The velocity is perpendicular to the field. Find the radius of the circle formed by the particle and also the time period.
A particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B, as shown in the figure. (a) Find the radius of the circular arc it describes in the magnetic field. (b) Find the angle subtended by the arc at the centre. (c) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.
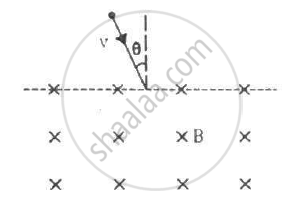
A proton is projected with a velocity of 3 × 106 m s−1 perpendicular to a uniform magnetic field of 0.6 T. Find the acceleration of the proton.
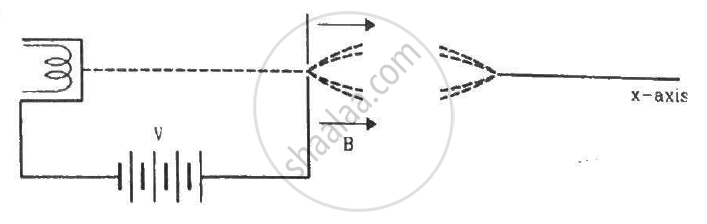
Electrons emitted with negligible speed from an electron gun are accelerated through a potential difference V along the x-axis. These electrons emerge from a narrow hole into a uniform magnetic field B directed along this axis. However, some of the electrons emerging from the hole make slightly divergent angles, as shown in the figure. Show that these paraxial electrons are refocussed on the x-axis at a distance `sqrt(8pi^2mV)/(eB^2).`
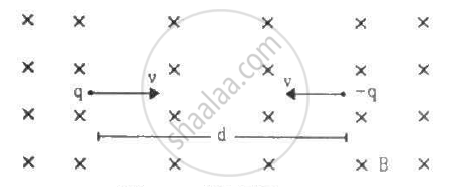
Two particles, each with mass m are placed at a separation d in a uniform magnetic field B, as shown in the figure. They have opposite charges of equal magnitude q. At time t = 0, the particles are projected towards each other, each with a speed v. Suppose the Coulomb force between the charges is switched off. (a) Find the maximum value vmof the projection speed, so that the two particles do not collide. (b) What would be the minimum and maximum separation between the particles if v = vm/2? (c) At what instant will a collision occur between the particles if v = 2vm? (d) Suppose v = 2vm and the collision between the particles is completely inelastic. Describe the motion after the collision.
A proton projected in a magnetic field of 0.020 T travels along a helical path of radius 5.0 cm and pitch 20 cm. Find the components of the velocity of the proton along and perpendicular to the magnetic field. Take the mass of the proton = 1.6 × 10−27 kg
A particle of mass m and charge q is released from the origin in a region in which the electric field and magnetic field are given by
`vecB = -B_0 vecj and vecE = E_0 vecK `
Find the speed of the particle as a function of its z-coordinate.
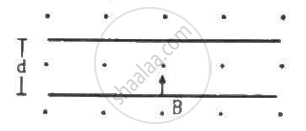
An electron is emitted with negligible speed from the negative plate of a parallel-plate capacitor charged to a potential difference V. The separation between the plates is dand a magnetic field B exists in the space, as shown in the figure. Show that the electron will fail to strike the upper plates if `d > ((2m_eV)/(eB_0^2))^(1/2)`
When does a moving charged particle nor experience any force while moving through a uniform magnetic field?
