Advertisements
Advertisements
Question
A long, straight wire carries a current along the z-axis, One can find two points in the x−y plane such that
(a) the magnetic fields are equal
(b) the directions of the magnetic fields are the same
(c) the magnitudes of the magnetic fields are equal
(d) the field at one point is opposite to that at the other point.
Solution
(b) the directions of the magnetic fields are the same
(c) the magnitudes of the magnetic fields are equal
(d) the field at one point is opposite to that at the other point.
Consider a current carrying wire lying along x axis.
At any two points on z axis which are at equal distance from the wire,one above the wire and one below the wire,the magnitude of magnetic field will be same and their directions will be opposite to each other.
At any two points on z axis which are at different distances from the wire,one above the wire and other also above the wire,the magnitude of magnetic field will be different and their directions will be same to each other.
APPEARS IN
RELATED QUESTIONS
Two infinitely long straight parallel wires, '1' and '2', carrying steady currents I1 and I2 in the same direction are separated by a distance d. Obtain the expression for the magnetic field `vecB`due to the wire '1' acting on wire '2'. Hence find out, with the help of a suitable diagram, the magnitude and direction of this force per unit length on wire '2' due to wire '1'. How does the nature of this force changes if the currents are in opposite direction? Use this expression to define the S.I. unit of current.
Using the concept of force between two infinitely long parallel current carrying conductors, define one ampere of current.
and ```vecE` and `vecB`denote electric and magnetic fields in a frame S and `vecE`→ and `vecB` in another frame S' moving with respect to S at a velocity `vecV` Two of the following equations are wrong. Identify them.
(a) `B_y^, = B_y + (vE_z)/c^2`
(b) `E_y^' = E_y - (vB_z)/(c^2)`
`(c) Ey = By + vE_z`
`(d) E_y = E_y + vB_z`
Two parallel, long wires carry currents i1 and i2 with i1 > i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 µT. If the direction of i2 is reversed, the field becomes 30 µT. The ratio i1/i2 is
A long, straight wire of radius R carries a current distributed uniformly over its cross section. T he magnitude of the magnetic field is
(a) maximum at the axis of the wire
(b) minimum at the axis of the wire
(c) maximum at the surface of the wire
(d) minimum at the surface of the wire.
A hypothetical magnetic field existing in a region is given by `vecB = B_0 vece` where `vece`_r denotes the unit vector along the radial direction. A circular loop of radius a, carrying a current i, is placed with its plane parallel to the x−y plane and the centre at (0, 0, d). Find the magnitude of the magnetic force acting on the loop.
A straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is µ. If the wire carries a current i, what minimum magnetic field should exist in the space in order to slide the wire on the rails?
The magnetic field existing in a region is given by `vecB = B_0(1 + x/1)veck` . A square loop of edge l and carrying a current i, is placed with its edges parallel to the x−y axes. Find the magnitude of the net magnetic force experienced by the loop.
Figure shows two parallel wires separated by a distance of 4.0 cm and carrying equal currents of 10 A along opposite directions. Find the magnitude of the magnetic field B at the points A1, A2, A3.

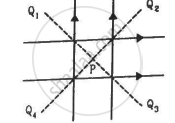
Four long, straight wires, each carrying a current of 5.0 A, are placed in a plane as shown in figure. The points of intersection form a square of side 5.0 cm.
(a) Find the magnetic field at the centre P of the square.
(b) Q1, Q2, Q3, and Q4, are points situated on the diagonals of the square and at a distance from P that is equal to the diagonal of the square. Find the magnetic fields at these points.
A long, straight wire carries a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. Consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the section B2 be the magnetic field at this point due to this second only. Find the value of d/l so that B2 differs from B1 by 1%.
A straight, how wire carries a current of 20 A. Another wire carrying equal current is placed parallel to it. If the force acting on a length of 10 cm of the second wire is 2.0 × 10−5 N, what is the separation between them?
If a current I is flowing in a straight wire parallel to x-axis and magnetic field is there in the y-axis then, ______.
Do magnetic forces obey Newton’s third law. Verify for two current elements dl1 = dlî located at the origin and dl2 = dlĵ located at (0, R, 0). Both carry current I.
Five long wires A, B, C, D and E, each carrying current I are arranged to form edges of a pentagonal prism as shown in figure. Each carries current out of the plane of paper.
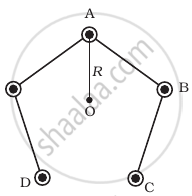
- What will be magnetic induction at a point on the axis O? AxisE is at a distance R from each wire.
- What will be the field if current in one of the wires (say A) is switched off?
- What if current in one of the wire (say) A is reversed?
Two long straight parallel current-carrying conductors are kept ‘a’ distant apart in the air. The direction of current in both the conductors is the same. Find the magnitude of force per unit length and the direction of the force between them. Hence define one ampere.
