Advertisements
Advertisements
Question
A long, straight wire carries a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. Consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the section B2 be the magnetic field at this point due to this second only. Find the value of d/l so that B2 differs from B1 by 1%.
Solution
Given:
Magnitude of current = i
Separation of the point from the wire = d

Thus, the magnetic field due to current in the long wire is given by
\[B_1 = \frac{\mu_0 i}{2\pi d}\]
Also, the magnetic field due to a section of length l on a perpendicular bisector is given by
\[\Rightarrow \frac{\mu_0 i l}{4\pi d}\frac{2}{d\sqrt{\frac{l^2}{d^2} + 4}}\]
\[\text{ Neglecting } \frac{l^2}{d^2} \left( \text{ very small } \right), \text{ we get } \]
\[ B_2 = \frac{\mu_0 i l}{4\pi d^2} \times \frac{2}{\sqrt{2}}\]
\[ = \frac{\sqrt{2} \mu_0 i l}{4\pi d^2}\]
Now,
B1 > B2
According to the question,
\[\frac{B_1 - B_2}{B_1} = \frac{1}{100}\]
\[ \Rightarrow B_2 = 0 . 99 B_1 \]
\[ \Rightarrow \frac{\sqrt{2} \mu_0 il}{4\pi d^2} = 0 . 99 \times \frac{\mu_0 i}{2\pi d}\]
\[ \Rightarrow \frac{d}{l}=\frac{1 . 414}{1 . 98}=0.71\]
APPEARS IN
RELATED QUESTIONS
Using the concept of force between two infinitely long parallel current carrying conductors, define one ampere of current.
Two long and parallel straight wires A and B carrying currents of 8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.
Derive the expression for force per unit length between two long straight parallel current carrying conductors. Hence define one ampere.
An electron beam projected along the positive x-axis deflects along the positive y-axis. If this deflection is caused by a magnetic field, what is the direction of the field? Can we conclude that the field is parallel to the z-axis?
An electron is moving along the positive x-axis. You want to apply a magnetic field for a short time so that the electron may reverse its direction and move parallel to the negative x-axis. This can be done by applying the magnetic field along
(a) y-axis
(b) z-axis
(c) y-axis only
(d) z-axis only
Two parallel, long wires carry currents i1 and i2 with i1 > i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 µT. If the direction of i2 is reversed, the field becomes 30 µT. The ratio i1/i2 is
A long, straight wire carries a current along the z-axis, One can find two points in the x−y plane such that
(a) the magnetic fields are equal
(b) the directions of the magnetic fields are the same
(c) the magnitudes of the magnetic fields are equal
(d) the field at one point is opposite to that at the other point.
A current of 10 A is established in a long wire along the positive z-axis. Find the magnetic field \[\vec{B}\] at the point (1 m, 0, 0).
A long, straight wire of radius r carries a current i and is placed horizontally in a uniform magnetic field B pointing vertically upward. The current is uniformly distributed over its cross section. (a) At what points will the resultant magnetic field have maximum magnitude? What will be the maximum magnitude? (b) What will be the minimum magnitude of the resultant magnetic field?
A straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is µ. If the wire carries a current i, what minimum magnetic field should exist in the space in order to slide the wire on the rails?
Figure shows a metallic wire of resistance 0.20 Ω sliding on a horizontal, U-shaped metallic rail. The separation between the parallel arms is 20 cm. An electric current of 2.0 µA passes through the wire when it is slid at a rate of 20 cm s−1. If the horizontal component of the earth's magnetic field is 3.0 × 10−5 T, calculate the dip at the place.
Figure shows two parallel wires separated by a distance of 4.0 cm and carrying equal currents of 10 A along opposite directions. Find the magnitude of the magnetic field B at the points A1, A2, A3.

Consider a 10-cm long piece of a wire which carries a current of 10 A. Find the magnitude of the magnetic field due to the piece at a point which makes an equilateral triangle with the ends of the piece.
Three coplanar parallel wires, each carrying a current of 10 A along the same direction, are placed with a separation 5.0 cm between the consecutive ones. Find the magnitude of the magnetic force per unit length acting on the wires.
According to Ampere's circuital law, ______.
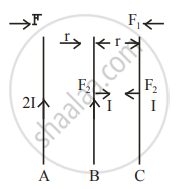
Three infinitely long parallel straight current-carrying wires A, B and C are kept at equal distance from each other as shown in the figure. The wire C experiences net force F. The net force on wire C, when the current in wire A is reversed will be ______.
Two long parallel wires kept 2 m apart carry 3A current each, in the same direction. The force per unit length on one wire due to the other is ______.
