Advertisements
Advertisements
Question
A proton and a deuteron having equal momenta enter in a region of a uniform magnetic field at right angle to the direction of a the field. Depict their trajectories in the field.
Solution
We know, Lorentz force, F = Bqv sinθ
where θ = angle between velocity of particle and magnetic field = 90o
So, Lorentz force, F = Bqv
Thus the particles will move in circular path.
`Bqv = (mv^2)/r ⇒ r = (mv)/(Bq)`
Let mp = mass of proton, md = mass of deuteron, vp = velocity of proton and
vd = velocity of deuteron
The charge of proton and deuteron are equal.
Given that mp vp = md vd
`r_p= (m_pv_p)/(Bq)` ................ (1)`
`r_d= (m_dv_d)/(Bq)` ................ (1)`
As (1) and (2) are equal , so rp = rd = r
Thus, the trajectory of both the particles will be same.
APPEARS IN
RELATED QUESTIONS
Show that the kinetic energy of the particle moving in a magnetic field remains constant.
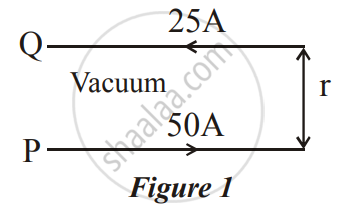
A long horizontal wire P carries a current of 50A. It is rigidly fixed. Another wire Q is placed directly above and parallel to P, as shown in Figure 1 below. The weight per unit length of the wire Q is 0.025 Nm-1 and it carries a current of 25A. Find the distance 'r' of the wire Q from the wire P so that the wire Q remains at rest
Write the expression for Lorentz magnetic force on a particle of charge ‘q’ moving with velocity `vecv` in a magnetic field`vecB`. Show that no work is done by this force on the charged particle.
Assume that the magnetic field is uniform in a cubical region and zero outside. Can you project a charged particle from outside into the field, so that the particle describes a complete circle in the field?
A beam consisting of protons and electrons moving at the same speed goes through a thin region in which there is a magnetic field perpendicular to the beam. The protons and the electrons
If a charged particle moves unaccelerated in a region containing electric and magnetic fields
(a) `vecE "must be perpendicular" to vecB`
(b) `vecv "must be perpendicular" to vecE`
(c) must be perpendicular to v_B
A magnetic field of \[(4.0\times10^-3 \overrightarrow k)\] T exerts a force of \[(4.0 \overrightarrow i + 3.0 \overrightarrow j ) \times 10^{−10} N\] on a particle with a charge of 1.0 × 10−9 C and going in the x − y plane. Find the velocity of the particle.
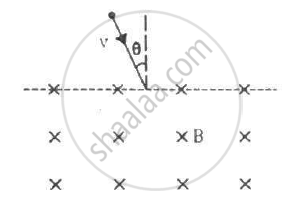
A particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B, as shown in the figure. (a) Find the radius of the circular arc it describes in the magnetic field. (b) Find the angle subtended by the arc at the centre. (c) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.
A uniform magnetic field of magnitude 0.20 T exists in space from east to west. With what speed should a particle of mass 0.010 g and with charge 1.0 × 10−5 C be projected from south to north so that it moves with uniform velocity?
A particle of mass m and charge q is released from the origin in a region in which the electric field and magnetic field are given by
`vecB = -B_0 vecj and vecE = E_0 vecK `
Find the speed of the particle as a function of its z-coordinate.
