Advertisements
Advertisements
Question
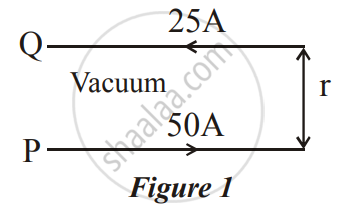
A long horizontal wire P carries a current of 50A. It is rigidly fixed. Another wire Q is placed directly above and parallel to P, as shown in Figure 1 below. The weight per unit length of the wire Q is 0.025 Nm-1 and it carries a current of 25A. Find the distance 'r' of the wire Q from the wire P so that the wire Q remains at rest
Solution
`F/l = mu_0/(4pi) (2I_1I_2)/r`
`0.025 = 10^(-7) xx (2xx50xx25)/r`
r = 0.01 m
APPEARS IN
RELATED QUESTIONS
Write the expression, in a vector form, for the Lorentz magnetic force \[\vec{F}\] due to a charge moving with velocity \[\vec{V}\] in a magnetic field \[\vec{B}\]. What is the direction of the magnetic force?
If a charged particle at rest experiences no electromagnetic force,
(a) the electric field must be zero
(b) the magnetic field must be zero
(c) the electric field may or may not be zero
(d) the magnetic field may or may not be zero
A magnetic field of \[(4.0\times10^-3 \overrightarrow k)\] T exerts a force of \[(4.0 \overrightarrow i + 3.0 \overrightarrow j ) \times 10^{−10} N\] on a particle with a charge of 1.0 × 10−9 C and going in the x − y plane. Find the velocity of the particle.
A 10 g bullet with a charge of 4.00 μC is fired at a speed of 270 m s−1 in a horizontal direction. A vertical magnetic field of 500 µT exists in the space. Find the deflection of the bullet due to the magnetic field as it travels through 100 m. Make appropriate approximations.
When a proton is released from rest in a room, it starts with an initial acceleration a0towards west. When it is projected towards north with a speed v0, it moves with an initial acceleration 3a0 towards west. Find the electric field and the maximum possible magnetic field in the room.
A metal wire PQ of mass 10 g lies at rest on two horizontal metal rails separated by 4.90 cm (figure). A vertically-downward magnetic field of magnitude 0.800 T exists in the space. The resistance of the circuit is slowly decreased and it is found that when the resistance goes below 20.0 Ω, the wire PQ starts sliding on the rails. Find the coefficient of friction.
A particle of charge 2.0 × 10−8 C and mass 2.0 × 10−10 g is projected with a speed of 2.0 × 103 m s−1 in a region with a uniform magnetic field of 0.10 T. The velocity is perpendicular to the field. Find the radius of the circle formed by the particle and also the time period.
A charged particle is accelerated through a potential difference of 12 kV and acquires a speed of 1.0 × 106 m s−1. It is then injected perpendicularly into a magnetic field of strength 0.2 T. Find the radius of the circle described by it.
A proton projected in a magnetic field of 0.020 T travels along a helical path of radius 5.0 cm and pitch 20 cm. Find the components of the velocity of the proton along and perpendicular to the magnetic field. Take the mass of the proton = 1.6 × 10−27 kg
An electron is emitted with negligible speed from the negative plate of a parallel-plate capacitor charged to a potential difference V. The separation between the plates is dand a magnetic field B exists in the space, as shown in the figure. Show that the electron will fail to strike the upper plates if `d > ((2m_eV)/(eB_0^2))^(1/2)`