Advertisements
Advertisements
Question
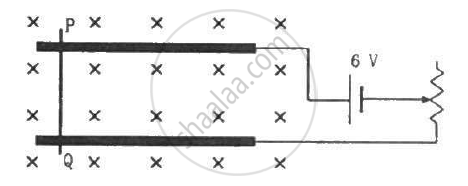
A metal wire PQ of mass 10 g lies at rest on two horizontal metal rails separated by 4.90 cm (figure). A vertically-downward magnetic field of magnitude 0.800 T exists in the space. The resistance of the circuit is slowly decreased and it is found that when the resistance goes below 20.0 Ω, the wire PQ starts sliding on the rails. Find the coefficient of friction.
Solution
Given:-
Mass of the metal wire, M = 10 g
Distance between the two horizontal metal rails, l = 4.90 cm
Vertically-downward magnetic field, B = 0.800 T
As per the question, when the resistance of the circuit is slowly decreased below 20.0 Ω, the wire PQ starts sliding on the rails. At that moment,
current in the wire, i = `V/R =6/20A `Using Fleming's left-hand rule, the magnetic force will act towards the right. So, due to this magnetic force, the wire will try to slide on the rails.The frictional force will try to oppose this motion of the wire.
When the wire just starts sliding on the rails, the frictional force acting on the wire will just balance the magnetic force acting on the wire.This implies
µR = F, where
µ is the coffiecent of friction
R is the normal reaction force and
F is the magnetic force
`⇒mu xx M xx g = ilB`
`muxx10xx10^-3xx9.8 = 6/20xx 4.9 xx 10^-2xx0.8`
`mu = (6xx4.9xx10^-2xx0.8)/(20xx10xx10^-3xx9.8)`
µ = 0.12
APPEARS IN
RELATED QUESTIONS
Write the expression, in a vector form, for the Lorentz magnetic force \[\vec{F}\] due to a charge moving with velocity \[\vec{V}\] in a magnetic field \[\vec{B}\]. What is the direction of the magnetic force?
Write the expression for the force `vecF` acting on a particle of mass m and charge q moving with velocity `vecV` in a magnetic field `vecB` , Under what conditions will it move in (i) a circular path and (ii) a helical path?
Show that the kinetic energy of the particle moving in a magnetic field remains constant.
A proton and an α-particle move perpendicular to a magnetic field. Find the ratio of radii of circular paths described by them when both have (i) equal velocities, and (ii) equal kinetic energy.
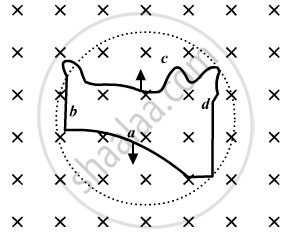
A flexible wire of irregular shape, abcd, as shown in the figure, turns into a circular shape when placed in a region of magnetic field which is directed normal to the plane of the loop away from the reader. Predict the direction of the induced current in the wire.
Write the expression for Lorentz magnetic force on a particle of charge ‘q’ moving with velocity `vecv` in a magnetic field`vecB`. Show that no work is done by this force on the charged particle.
Assume that the magnetic field is uniform in a cubical region and zero outside. Can you project a charged particle from outside into the field, so that the particle describes a complete circle in the field?
A charged particle moves in a gravity-free space without change in velocity. Which of the following is/are possible?
(a) E = 0, B = 0
(b) E = 0, B ≠ 0
(c) E ≠ 0, B = 0
(d) E ≠ 0, B ≠ 0
A charged particle moves along a circle under the action of possible constant electric and magnetic fields. Which of the following is possible?
(a) E = 0, B = 0
(b) E = 0, B ≠ 0
(c) E ≠ 0, B = 0
(d) E ≠ 0, B ≠ 0
Two ions have equal masses but one is singly-ionised and the other is doubly-ionised. They are projected from the same place in a uniform magnetic field with the same velocity perpendicular to the field.
(a) Both ions will move along circles of equal radii.
(b) The circle described by the singly-ionised charge will have a radius that is double that of the other circle.
(c) The two circles do not touch each other.
(d) The two circles touch each other.
A wire, carrying a current i, is kept in the x−y plane along the curve y = A sin `((2x)/lamda x)`. magnetic field B exists in the z direction. Find the magnitude of the magnetic force on the portion of the wire between x = 0 and x = λ.
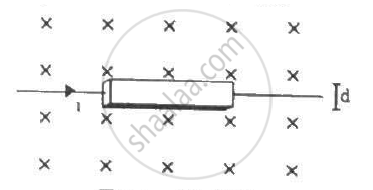
A current i is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n. (a) Find the drift velocity v of the electrons. (b) If a magnetic field B exists in the region, as shown in the figure, what is the average magnetic force on the free electrons? (c) Due to the magnetic force, the free electrons get accumulated on one side of the conductor along its length. This produces a transverse electric field in the conductor, which opposes the magnetic force on the electrons. Find the magnitude of the electric field which will stop further accumulation of electrons. (d) What will be the potential difference developed across the width of the conductor due to the electron-accumulation? The appearance of a transverse emf, when a current-carrying wire is placed in a magnetic field, is called Hall effect.
Protons with kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field, so that it just misses a plane target kept at a distance l in front of the accelerator. Find the magnetic field.
A circular coil of radius 2.0 cm has 500 turns and carries a current of 1.0 A. Its axis makes an angle of 30° with the uniform magnetic field of magnitude 0.40 T that exists in the space. Find the torque acting on the coil.
A square coil of edge l and with n turns carries a current i. It is kept on a smooth horizontal plate. A uniform magnetic field B exists parallel to an edge. The total mass of the coil is M. What should be the minimum value of B for which the coil will start tipping over?
A proton is projected with a velocity of 3 × 106 m s−1 perpendicular to a uniform magnetic field of 0.6 T. Find the acceleration of the proton.
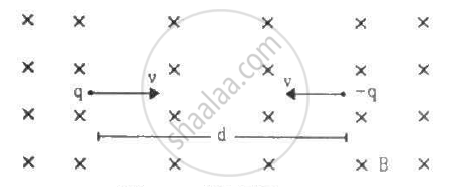
Two particles, each with mass m are placed at a separation d in a uniform magnetic field B, as shown in the figure. They have opposite charges of equal magnitude q. At time t = 0, the particles are projected towards each other, each with a speed v. Suppose the Coulomb force between the charges is switched off. (a) Find the maximum value vmof the projection speed, so that the two particles do not collide. (b) What would be the minimum and maximum separation between the particles if v = vm/2? (c) At what instant will a collision occur between the particles if v = 2vm? (d) Suppose v = 2vm and the collision between the particles is completely inelastic. Describe the motion after the collision.
A particle moves in a circle of diameter 1.0 cm under the action of a magnetic field of 0.40 T. An electric field of 200 V m−1 makes the path straight. Find the charge/mass ratio of the particle.
A proton projected in a magnetic field of 0.020 T travels along a helical path of radius 5.0 cm and pitch 20 cm. Find the components of the velocity of the proton along and perpendicular to the magnetic field. Take the mass of the proton = 1.6 × 10−27 kg
