Advertisements
Advertisements
Question
A positively-charged particle projected towards east is deflected towards north by a magnetic field. The field may be
Options
towards west
towards south
upwards
downwards
Solution
downwards
A positively-charged particle projected towards east can be considered as current in the eastern direction. Here, the positive charge is deflected towards the north by a magnetic field, i.e. the positively-charged particle experiences a force in the northern direction.
Hence, in order to determine the direction of the magnetic field, we apply Fleming's left-hand rule. According to this rule, when we stretch the thumb, the fore-finger and the middle finger mutually perpendicular to each other, then the thumb gives the direction of the force experienced by the charged particle, the fore-finger gives the direction of the magnetic field and the middle finger gives the direction of the current. Thus, if we direct the middle finger in the eastern direction, the thumb in the northern direction, we see that the fore-finger points in the downward direction.
Thus, the direction of the magnetic field is found to be in the downward direction.
APPEARS IN
RELATED QUESTIONS
Show that the kinetic energy of the particle moving in a magnetic field remains constant.
A moving charged particle q travelling along the positive x-axis enters a uniform magnetic field B.
When will the force acting on q be maximum?
A proton and a deuteron having equal momenta enter in a region of a uniform magnetic field at right angle to the direction of a the field. Depict their trajectories in the field.
A beam consisting of protons and electrons moving at the same speed goes through a thin region in which there is a magnetic field perpendicular to the beam. The protons and the electrons
If a charged particle projected in a gravity-free room deflects,
(a) there must be an electric field
(b) there must be a magnetic field
(c) both fields cannot be zero
(d) both fields can be non-zero
A charged particle moves in a gravity-free space without change in velocity. Which of the following is/are possible?
(a) E = 0, B = 0
(b) E = 0, B ≠ 0
(c) E ≠ 0, B = 0
(d) E ≠ 0, B ≠ 0
A charged particle moves along a circle under the action of possible constant electric and magnetic fields. Which of the following is possible?
(a) E = 0, B = 0
(b) E = 0, B ≠ 0
(c) E ≠ 0, B = 0
(d) E ≠ 0, B ≠ 0
If a charged particle moves unaccelerated in a region containing electric and magnetic fields
(a) `vecE "must be perpendicular" to vecB`
(b) `vecv "must be perpendicular" to vecE`
(c) must be perpendicular to v_B
Prove that the force acting on a current-carrying wire, joining two fixed points a and b in a uniform magnetic field, is independent of the shape of the wire.
A wire, carrying a current i, is kept in the x−y plane along the curve y = A sin `((2x)/lamda x)`. magnetic field B exists in the z direction. Find the magnitude of the magnetic force on the portion of the wire between x = 0 and x = λ.
A metal wire PQ of mass 10 g lies at rest on two horizontal metal rails separated by 4.90 cm (figure). A vertically-downward magnetic field of magnitude 0.800 T exists in the space. The resistance of the circuit is slowly decreased and it is found that when the resistance goes below 20.0 Ω, the wire PQ starts sliding on the rails. Find the coefficient of friction.
A proton describes a circle of radius 1 cm in a magnetic field of strength 0.10 T. What would be the radius of the circle described by an α-particle moving with the same speed in the same magnetic field?
Consider a non-conducting ring of radius r and mass m that has a total charge qdistributed uniformly on it. The ring is rotated about its axis with an angular speed ω. (a) Find the equivalent electric current in the ring. (b) Find the magnetic moment µ of the ring. (c) Show that `pi = (q)/(2m)` l, where l is the angular momentum of the ring about its axis of rotation.
A particle of mass m and charge q is projected into a region that has a perpendicular magnetic field B. Find the angle of deviation (figure) of the particle as it comes out of the magnetic field if the width d of the region is very slightly smaller than
(a) `(mv)/(qB)` (b)`(mv)/(2qB)` (c)`(2mv)/(qB)`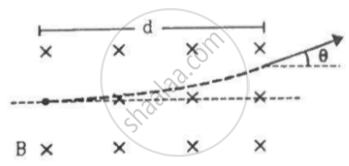
A narrow beam of singly-charged carbon ions, moving at a constant velocity of 6.0 × 104m s−1, is sent perpendicularly in a rectangular region of uniform magnetic field B = 0.5 T (figure). It is found that two beams emerge from the field in the backward direction, the separations from the incident beam being 3.0 cm and 3.5 cm. Identify the isotopes present in the ion beam. Take the mass of an ion = A(1.6 × 10−27) kg, where A is the mass number.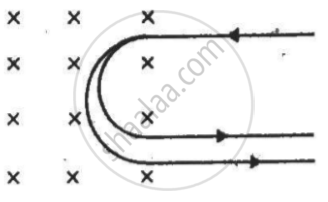
A proton is projected with a velocity of 3 × 106 m s−1 perpendicular to a uniform magnetic field of 0.6 T. Find the acceleration of the proton.
A particle moves in a circle of diameter 1.0 cm under the action of a magnetic field of 0.40 T. An electric field of 200 V m−1 makes the path straight. Find the charge/mass ratio of the particle.
When does a moving charged particle nor experience any force while moving through a uniform magnetic field?
