Advertisements
Advertisements
प्रश्न
A lot consists of 144 ballpoint pens of which 20 are defective and others good. Tanvy will buy a pen if it is good, but will not buy it if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that she will buy it,
उत्तर
Total number of pens = 144
Number of defective pens = 20
Number of good pens = 144 − 20 = 124
Let E1 be the event of getting a good pen.
∴ P(buying a pen) = P(E1) = `("Number of outcomes favourable to" E_4)/ "Number of all possible outcome" `
`124/144 = 31/36`
Thus, the probability that Tanvy will buy a pen is `31/36`
APPEARS IN
संबंधित प्रश्न
A card is drawn at random from a well-shuffled deck of playing cards. Find the probability that the card drawn is a card of spade or an ace.
Rahim tosses two different coins simultaneously. Find the probability of getting at least one tail.
Find the class mark of the class 35 - 39.
A game consist of tossing a one-rupee coin 3 times and noting the outcome each time. Ramesh will win the game if all the tosses show the same result, (i.e. either all thee heads or all three tails) and loses the game otherwise. Find the probability that Ramesh will lose the game.
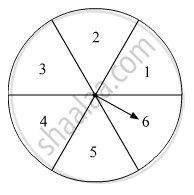
In fig. 7 is shown a disc on which a player spins an arrow twice. The fraction `a/b` is formed, where 'a' is the number of sector on which arrow stops on the first spin and 'b' is the number of the sector in which the arrow stops on second spin. On each spin, each sector has equal chance of selection by the arrow. Find the probability that the fraction `a/b>1.`
Two dice are thrown together. The probability of getting the same number on both dice is.
A box contains 5 red, 8 blue and 3 green pens. Rutuja wants to pick a pen at random. What is the probability that the pen is blue?
A box contains 20 cards numbered from 1 to 20. A card is drawn at random from the box. Find the probability that the number on the drawn card is divisible by 2 or 3
All jacks, queens and kings are removed from a pack of 52 cards. The remaining cards are well-shuffled and then a card is randomly drawn from it. Find the probability that this card is a red card.
A bag contains 4 white balls, 5 red balls, 2 black balls and 4 green balls. A ball is drawn at random from the bag. Find the probability that it is red or white.
Five cards − the ten, jack, queen, king and ace of diamonds are well shuffled with their faces downwards. One card is then picked up at random. What is the probability that the drawn card is the queeen?
A game consists of tossing a one-rupee coin three times, and noting its outcome each time. Find the probability of getting three heads.
A bag contains 4 red and 6 black balls. A ball is taken out of the bag at random. What is the probability of getting a black ball?
Three different coins are tossed simultaneously. Find the probability of getting exactly one head.
There are 24 balls in a pot. If 3 of them are Red, 5 of them are Blue and the remaining are Green then, what is the probability of picking out a Green ball?
In a throw of a dice, the probability of getting the number 7 is ______.
The probability of getting a prime number is the same as that of a composite number in a throw of a dice.
A dice is rolled once. What is the probability that the number on top will be less than 1
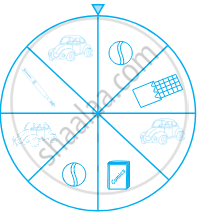
At a Birthday Party, the children spin a wheel to get a gift. Find the probability of getting a ball
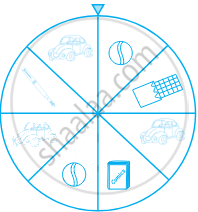
At a Birthday Party, the children spin a wheel to get a gift. Find the probability of any toy except a chocolate