Advertisements
Advertisements
प्रश्न
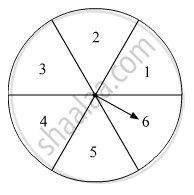
In fig. 7 is shown a disc on which a player spins an arrow twice. The fraction `a/b` is formed, where 'a' is the number of sector on which arrow stops on the first spin and 'b' is the number of the sector in which the arrow stops on second spin. On each spin, each sector has equal chance of selection by the arrow. Find the probability that the fraction `a/b>1.`
उत्तर १
Elementary events associated with the experiment of spinning an arrow twice on a disc are
(1, 1), (1, 2), ...,(1, 6)
(2, 1), (2, 2), ...,(2, 6)
(3, 1), (3, 2), ...,(3, 6)
(4, 1), (4, 2), ...,(4, 6)
(5, 1), (5, 2), ...,(5, 6)
(6, 1), (6, 2), ...,(6, 6)
∴ Total number of elementary events = 36
It is given that a is the number of sector on which the arrow stops on the first spin and b is the number of the sector on which the arrow stops on the second spin.
Let A denote the event `a/b>1.`
Now,
`a/b>1Rightarrow a>b`
So, elementary events favourable to the event A are
(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3), (6, 4) and (6, 5)
∴ Total number of favourable events = 15
Thus,
Required probability =`"(The number of favourable events)"/"(Total number of the events)"=15/36 =5/12`
उत्तर २
Elementary events associated with the experiment of spinning an arrow twice on a disc are
(1, 1), (1, 2), ...,(1, 6)
(2, 1), (2, 2), ...,(2, 6)
(3, 1), (3, 2), ...,(3, 6)
(4, 1), (4, 2), ...,(4, 6)
(5, 1), (5, 2), ...,(5, 6)
(6, 1), (6, 2), ...,(6, 6)
∴ Total number of elementary events = 36
It is given that a is the number of sector on which the arrow stops on the first spin and b is the number of the sector on which the arrow stops on the second spin.
Let A denote the event `a/b>1.`
Now,
`a/b>1Rightarrow a>b`
So, elementary events favourable to the event A are
(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3), (6, 4) and (6, 5)
∴ Total number of favourable events = 15
Thus,
Required probability =`"(The number of favourable events)"/"(Total number of the events)"=15/36 =5/12`
APPEARS IN
संबंधित प्रश्न
In a certain race, there are three boys A, B, C. The winning probability of A is twice than B and the winning probability of B is twice than C. If P(A) + P(B) + P(C) = 1, then find the probability of win for each boy.
Cards marked with number 3, 4, 5, ...., 50 are placed in a box and mixed thoroughly. A card is drawn at random form the box. Find the probability that the selected card bears a perfect square number.
A bag contains 18 balls out of which x balls are red.
(i) If one ball is drawn at random from the bag, what is the probability that it is not red?
(ii) If 2 more red balls are put in the bag, the probability of drawing a red ball will be `9/8` times the probability of drawing a red ball in the first case. Find the value of x.
Which number cannot represent a probability?
A box contains 5 red marbels, 8 white marbles and 4 green marbles, One marble is taken out of the box at ramdom. What is the probability that the marble taken out will be not green?
Cards numbered from 11 to 60 are kept in a box. If a card is drawn at random from the box, find the probability that the number on the drawn card is an odd number
If \[\bar{E}\] denote the complement or negation of an even E, what is the value of P(E) + P(\[\bar{E}\]) ?
What is the probability that a non-leap year has 53 Sundays?
What is the probability that a leap year has 52 Mondays?
A lot consists of 144 ballpoint pens of which 20 are defective and others good. Tanvy will buy a pen if it is good, but will not buy it if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that she will not buy it?
A box contains cards bearing numbers 6 to 70. If one card is drawn at random from the box, find the probability that it bears a composite number between 50 and 70.
A die is thrown once. Find the probability of getting a number which is a prime number
A game consists of tossing a coin 3 times and noting the outcome each time. If getting the same result in all the tosses is a success, find the probability of losing the game.
A coin is tossed twice. Find the probability of getting: two tails
A bag contains 3 white, 5 black, and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is a white ball.
Two coins are tossed together. What is the probability of getting:
(i) at least one head
(ii) both heads or both tails.
Two coins are tossed together. Find the probability of getting: exactly one tail
Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is: less than 12
On throwing a dice once, the probability of occurence of an even number is `1/2`.
A dice is rolled once. What is the probability that the number on top will be a factor of 6
