Advertisements
Advertisements
प्रश्न
The co-ordinates of the points A, B and C are (6, 3), (−3, 5) and (4, −2) respectively. P(x, y) is any point in the plane. Show that \[\frac{ar\left( ∆ PBC \right)}{ar\left( ∆ ABC \right)} = \left| \frac{x + y - 2}{7} \right|\]
उत्तर
We know that the area of a triangle having vertices (x1, y1), (x2, y2) and (x3, y3) is\[\frac{1}{2}\left| x_1 \left( y_2 - y_3 \right) + x_2 \left( y_3 - y_1 \right) + x_3 \left( y_1 - y_2 \right) \right|\]
Area of ∆PBC
\[ = \frac{1}{2}\left| 7x + 7y - 14 \right|\]
\[ = \frac{7}{2}\left| x + y - 2 \right| \text{square units}\]
\[ = \frac{1}{2}\left| 42 + 15 - 8 \right|\]
\[ = \frac{49}{2} \text{square units}\]
\[ \Rightarrow \frac{ar\left( ∆ PBC \right)}{ar\left( ∆ ABC \right)} = \frac{\left| x + y - 2 \right|}{7} = \left| \frac{x + y - 2}{7} \right|\]
APPEARS IN
संबंधित प्रश्न
If the sides of a triangle are 3 cm, 4 cm, and 6 cm long, determine whether the triangle is a right-angled triangle.
The sides of triangle is given below. Determine it is right triangle or not.
a = 7 cm, b = 24 cm and c = 25 cm
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
ABCD is a square. F is the mid-point of AB. BE is one third of BC. If the area of ΔFBE = 108 cm2, find the length of AC.
Calculate the height of an equilateral triangle each of whose sides measures 12 cm.
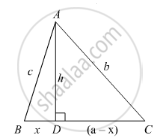
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
∆ABD is a right triangle right-angled at A and AC ⊥ BD. Show that
(i) AB2 = BC x BD
(ii) AC2 = BC x DC
(iii) AD2 = BD x CD
(iv) `"AB"^2/"AC"^2="BD"/"DC"`
State the converse of Pythagoras theorem.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
