Advertisements
Advertisements
प्रश्न
∆ABD is a right triangle right-angled at A and AC ⊥ BD. Show that
(i) AB2 = BC x BD
(ii) AC2 = BC x DC
(iii) AD2 = BD x CD
(iv) `"AB"^2/"AC"^2="BD"/"DC"`
उत्तर
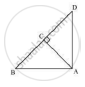
(i) In ΔADB and ΔCAB
∠DAB = ∠ACB = 90°
∠ABD = ∠CBA (common angle)
∠ADB = ∠CAB (remaining angle)
So, ΔADB ~ ΔCAB (by AAA similarity)
Therefore `"AB"/"CB"="BD"/"AB"`
⇒ AB2 = CB × BD
(ii) Let ∠CAB = x
In ΔCBA
∠CBA = 180° − 90° − 𝑥
∠CBA = 90° − 𝑥
Similarly in ΔCAD
∠CAD = 90° − ∠CAD = 90° − 𝑥
∠CDA = 90° − ∠CAB
= 90° − 𝑥
∠CDA = 180° −90° − (90° − 𝑥)
∠CDA = x
Now in ΔCBA and ΔCAD we may observe that
∠CBA = ∠CAD
∠CAB = ∠CDA
∠ACB = ∠DCA = 90°
Therefore ΔCBA ~ ΔCAD (by AAA rule)
Therefore `"AC"/"DC"="BC"/"AC"`
⇒ AC2 = DC × BC
(iii) In ΔDCA & ΔDAB
∠DCA = ∠DAB (both are equal to 90°)
∠CDA = ∠ADB (common angle)
∠DAC = ∠DBA (remaining angle)
ΔDCA ~ ΔDAB (AAA property)
Therefore `"DC"/"DA"="DA"/"DB"`
⇒AD2 = BD × CD
(iv) From part (i) 𝐴𝐵2 = 𝐶𝐵 × 𝐵𝐷
From part (ii) 𝐴𝐶2 = 𝐷𝐶 × 𝐵𝐶
Hence `"AB"^2/"AC"^2=(CBxxBD)/(DCxxBC)`
`"AB"^2/"AC"^2="BD"/"DC"`
Hence proved
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 9 cm, b = l6 cm and c = 18 cm
The sides of triangle is given below. Determine it is right triangle or not.
a = 8 cm, b = 10 cm and c = 6 cm
In Figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED
= x, AD = p and AE = h, prove that:
(i) `b^2 = p^2 + ax + a^2/4`
(ii) `c^2 = p^2 - ax + a^2/4`
(iii) `b^2 + c^2 = 2p^2 + a^2/2`
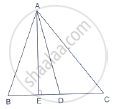
In a right ∆ABC right-angled at C, if D is the mid-point of BC, prove that BC2 = 4(AD2 − AC2).
Determine whether the triangle having sides (a − 1) cm, 2`sqrta` cm and (a + 1) cm is a right-angled
triangle.
If D, E, F are the respectively the midpoints of sides BC, CA and AB of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
A man goes 12m due south and then 35m due west. How far is he from the starting point.
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `5sqrt(2)` , then what is the height of ∆ABC?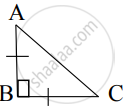
A girl walks 200m towards East and then 150m towards North. The distance of the girl from the starting point is ______.
Find the altitude of an equilateral triangle of side 8 cm.
