Advertisements
Advertisements
प्रश्न
In an equilateral ΔABC, AD ⊥ BC, prove that AD2 = 3BD2.
उत्तर
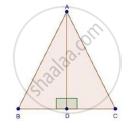
We have, ΔABC is an equilateral Δ and AD ⊥ BC
In ΔADB and ΔADC
∠ADB = ∠ADC [Each 90°]
AB = AC [Given]
AD = AD [Common]
Then, ΔADB ≅ ΔADC [By RHS condition]
∴ BD = CD =BC/2 .......(i) [corresponding parts of similar Δ are proportional]
In, ΔABD, by Pythagoras theorem
AB2 = AD2 + BD2
⇒ BC2 = AD2 + BD2 [AB = BC given]
⇒ [2BD]2 = AD2 + BD2 [From (i)]
⇒ 4BD2 − BD2 = AD2
⇒ 3BD2 = AD2
APPEARS IN
संबंधित प्रश्न
If the sides of a triangle are 3 cm, 4 cm, and 6 cm long, determine whether the triangle is a right-angled triangle.
A man goes 15 metres due west and then 8 metres due north. How far is he from the starting point?
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
Using Pythagoras theorem determine the length of AD in terms of b and c shown in Figure.
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
Calculate the height of an equilateral triangle each of whose sides measures 12 cm.
In Figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED
= x, AD = p and AE = h, prove that:
(i) `b^2 = p^2 + ax + a^2/4`
(ii) `c^2 = p^2 - ax + a^2/4`
(iii) `b^2 + c^2 = 2p^2 + a^2/2`
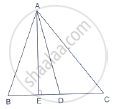
In a quadrilateral ABCD, ∠B = 90°, AD2 = AB2 + BC2 + CD2, prove that ∠ACD = 90°.
State Pythagoras theorem
From given figure, In ∆ABC, AB ⊥ BC, AB = BC then m∠A = ?