Advertisements
Advertisements
प्रश्न
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
उत्तर
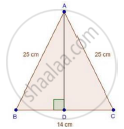
We have
AB = AC = 25 cm and BC = 14 cm
In ΔABD and ΔACD
∠ADB = ∠ADC [Each 90°]
AB = AC [Each 25 cm]
AD = AD [Common]
Then, ΔABD ≅ ΔACD [By RHS condition]
∴ BD = CD = 7 cm [By c.p.c.t]
In ΔADB, by Pythagoras theorem
AD2 + BD2 = AB2
⇒ AD2 + 72 = 252
⇒ AD2 = 625 − 49 = 576
⇒ AD = `sqrt576` = 24 cm
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 9 cm, b = l6 cm and c = 18 cm
The sides of triangle is given below. Determine it is right triangle or not.
a = 8 cm, b = 10 cm and c = 6 cm
In a ΔABC, AB = BC = CA = 2a and AD ⊥ BC. Prove that
(i) AD = a`sqrt3`
(ii) Area (ΔABC) = `sqrt3` a2
The lengths of the diagonals of a rhombus are 24 cm and 10 cm. Find each side of the rhombus.
Calculate the height of an equilateral triangle each of whose sides measures 12 cm.
In ∆ABC, ∠A is obtuse, PB ⊥ AC and QC ⊥ AB. Prove that:
(i) AB ✕ AQ = AC ✕ AP
(ii) BC2 = (AC ✕ CP + AB ✕ BQ)
State Pythagoras theorem
ΔABC~ΔDEF such that ar(ΔABC) = 64 cm2 and ar(ΔDEF) = `169cm^2`. If BC = 4cm, find EF.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
Find the altitude of an equilateral triangle of side 8 cm.
