Advertisements
Advertisements
प्रश्न
Find the altitude of an equilateral triangle of side 8 cm.
उत्तर
Let ABC be an equilateral triangle of side 8 cm
AB = BC = CA = 8 cm ...(All sides of an equilateral triangle is equal)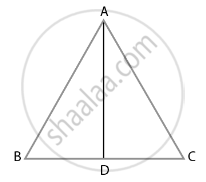
Draw altitude AD which is perpendicular to BC.
Then, D is the mid-point of BC.
∴ BD = CD = `1/2`
BC = `8/2` = 4 cm
Now, by Pythagoras theorem
AB2 = AD2 + BD2
⇒ (8)2 = AD2 + (4)2
⇒ 64 = AD2 + 16
⇒ AD = 64 – 16 = 48
⇒ AD = `sqrt(48)` = `4sqrt(3)` cm.
Hence, altitude of an equilateral triangle is `4sqrt(3)` cm.
APPEARS IN
संबंधित प्रश्न
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
ABCD is a square. F is the mid-point of AB. BE is one third of BC. If the area of ΔFBE = 108 cm2, find the length of AC.
In a ΔABC, AB = BC = CA = 2a and AD ⊥ BC. Prove that
(i) AD = a`sqrt3`
(ii) Area (ΔABC) = `sqrt3` a2
Each side of a rhombus is 10 cm. If one of its diagonals is 16 cm find the length of the other diagonal.
In right-angled triangle ABC in which ∠C = 90°, if D is the mid-point of BC, prove that AB2 = 4AD2 − 3AC2.
In a quadrilateral ABCD, ∠B = 90°, AD2 = AB2 + BC2 + CD2, prove that ∠ACD = 90°.
An aeroplane leaves an airport and flies due north at a speed of 1000km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/hr. How far apart will be the two planes after 1 hours?
The co-ordinates of the points A, B and C are (6, 3), (−3, 5) and (4, −2) respectively. P(x, y) is any point in the plane. Show that \[\frac{ar\left( ∆ PBC \right)}{ar\left( ∆ ABC \right)} = \left| \frac{x + y - 2}{7} \right|\]
Find the side and perimeter of a square whose diagonal is `13sqrt2` cm.
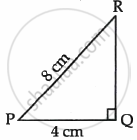
In the given figure, ΔPQR is a right triangle right angled at Q. If PQ = 4 cm and PR = 8 cm, then P is ______.