Advertisements
Advertisements
प्रश्न
If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ∆ABC.
उत्तर
According to the question,
AB = 4 cm,
DE = 6 cm
EF = 9 cm
FD = 12 cm
Also,
∆ABC ∼ ∆DEF
We have,
∴ `("AB")/("ED") = ("BC")/("EF") = ("AC")/("DF")`
⇒ `4/6 = ("BC")/9 = ("AC")/12`
By taking first two terms, we have
⇒ `4/6 = ("BC")/9`
⇒ BC = `((4 xx 9))/6` = 6 cm
And by taking last two terms, we have,
`("BC")/9 = ("AC")/12`
`6/9 = ("AC")/12`
AC = `(6 xx 12)/9` = 8 cm
Now,
Perimeter of ∆ABC
= AB + BC + AC
= 4 + 6 + 8
= 18 cm
Thus, the perimeter of the triangle is 18 cm.
APPEARS IN
संबंधित प्रश्न
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
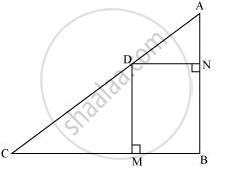
In the given figure, D is a point on hypotenuse AC of ΔABC, DM ⊥ BC and DN ⊥ AB, Prove that:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN
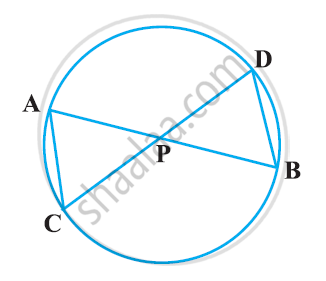
In the given figure, two chords AB and CD intersect each other at the point P. prove that:
(i) ΔAPC ∼ ΔDPB
(ii) AP.BP = CP.DP
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
In a trapezium ABCD, it is given that AB║CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB) = 84cm2. Find ar(ΔCOD).
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
In the given figure, ΔLMN is similar to ΔPQR. To find the measure of ∠N, complete the following activity.
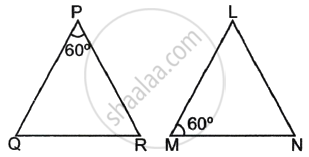
Given: ΔLMN ∼ ΔPQR
Since ΔLMN ∼ ΔPQR, therefore, corresponding angles are equal.
So, ∠L ≅ `square`
⇒ ∠L = `square`
We know, the sum of angles of a triangle = `square`
∴ ∠L + ∠M + ∠N = `square`
Substituting the values of ∠L and ∠M in equation (i),
`square` + `square` + ∠N = `square`
∠N + `square` = `square`
∠N = `square` – `square`
∠N = `square`
Hence, the measure of ∠N is `square`.
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
