Advertisements
Advertisements
प्रश्न
In the given figure, two chords AB and CD intersect each other at the point P. prove that:
(i) ΔAPC ∼ ΔDPB
(ii) AP.BP = CP.DP
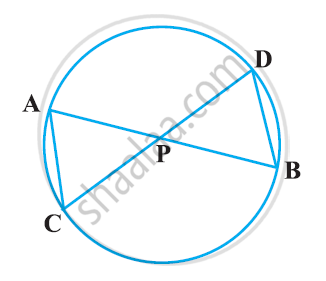
उत्तर
Let us join CB.
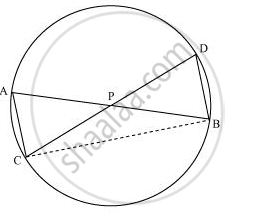
(i) In ΔAPC and ΔDPB,
∠APC = ∠DPB (Vertically opposite angles)
∠CAP = ∠BDP (Angles in the same segment for chord CB)
ΔAPC ∼ ΔDPB (By AA similarity criterion)
(ii) We have already proved that
ΔAPC ∼ ΔDPB
We know that the corresponding sides of similar triangles are proportional.
`:. (AP)/(DP) = (PC)/(PB) = (CA)/(BD)`
`=>(AP)/(DP) = (PC)/(PB)`
∴ AP. PB = PC. DP
APPEARS IN
संबंधित प्रश्न
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

The sides of certain triangles are given below. Determine which of them right triangles are.
1.6cm, 3.8cm, 4cm
State the AAA-similarity criterion
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

In the given figure, value of x(in cm) is

If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.
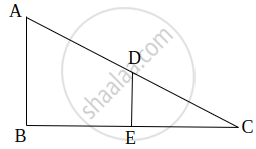
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
