Advertisements
Advertisements
प्रश्न
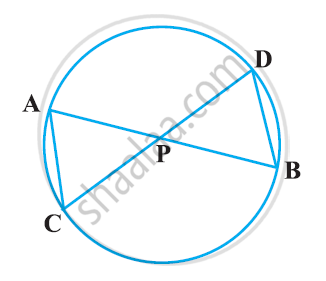
In the given figure, two chords AB and CD intersect each other at the point P. prove that:
(i) ΔAPC ∼ ΔDPB
(ii) AP.BP = CP.DP
उत्तर
Let us join CB.
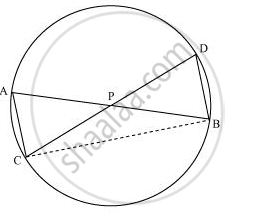
(i) In ΔAPC and ΔDPB,
∠APC = ∠DPB (Vertically opposite angles)
∠CAP = ∠BDP (Angles in the same segment for chord CB)
ΔAPC ∼ ΔDPB (By AA similarity criterion)
(ii) We have already proved that
ΔAPC ∼ ΔDPB
We know that the corresponding sides of similar triangles are proportional.
`:. (AP)/(DP) = (PC)/(PB) = (CA)/(BD)`
`=>(AP)/(DP) = (PC)/(PB)`
∴ AP. PB = PC. DP
APPEARS IN
संबंधित प्रश्न
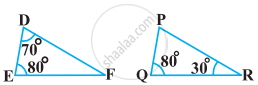
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
In figure, if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.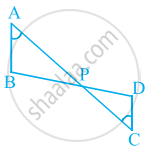
Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.
