Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
उत्तर
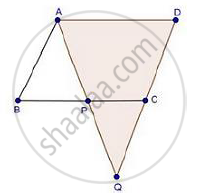
Given: ABCD is a parallelogram
To prove: BP × DQ = AB × BC
Proof: In ΔABP and ΔQDA
∠B = ∠D [Opposite angles of parallelogram]
∠BAP = ∠AQD [Alternate interior angles]
Then, ΔABP ~ ΔQDA [By AA similarity]
`therefore"AB"/"QD"="BP"/"DA"` [Corresponding parts of similar Δ are proportional]
But, DA = BC [Opposite sides of parallelogram]
Then, `therefore"AB"/"QD"="BP"/"BC"`
⇒ AB × BC = QD × BP
APPEARS IN
संबंधित प्रश्न
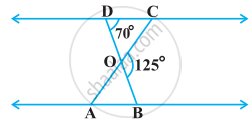
In the following figure, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
In the following figure, AB || QR. Find the length of PB.

In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

The sides of certain triangles are given below. Determine which of them right triangles are.
7cm, 24cm, 25cm
The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
In the given figure, value of x(in cm) is

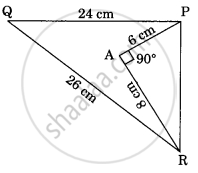
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
In figure, if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.
In the given figure, DE ∥ BC, AE = a units, EC = b units, DE = x units and BC = y units. Which of the following is true?